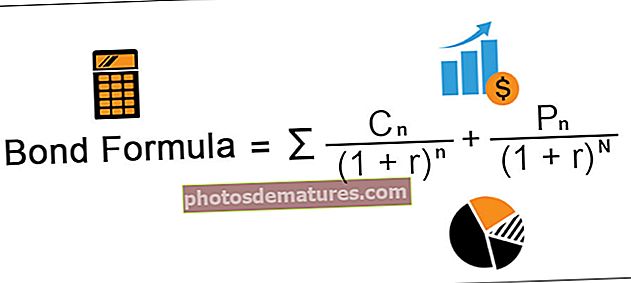相关系数(定义,公式)|如何计算?
什么是相关系数?
相关系数用于确定两个变量之间的关系有多强,其值的范围可以从-1.0到1.0,其中-1.0表示负相关,而+1.0表示正相关。它考虑变量中的相对运动,然后定义它们之间是否存在任何关系。
相关系数公式


在哪里
- r =相关系数
- n =观察数
- x =上下文中的第一个变量
- y =第二个变量
解释
如果两个变量之间存在任何相关性或说是相互关系,则应指出其中一个变量的值是否发生变化,然后另一个变量的值也趋于变化,具体说来可能是相同的,也可能是相反的。 。等式的分子部分进行变量一起移动的测试和相对强度,等式的分母部分通过将变量与平方变量的差相乘来缩放分子。
例子
您可以在此处下载此相关系数公式Excel模板–相关系数公式Excel模板范例#1
考虑以下两个变量x和y,需要计算相关系数。
以下是用于计算的数据

解决方案:
使用上面的等式,我们可以计算出以下内容

我们具有上表中的所有值,其中n = 4。
现在,输入用于计算相关系数的值。

因此,计算如下

r =(4 * 25,032.24)–(262.55 * 317.31)/√[(4 * 20,855.74)–(262.55)2] * [(4 * 30,058.55)–(317.31)2]
r = 16,820.21 / 16,831.57
系数将是–

系数= 0.99932640
范例#2
X国是一个成长中的经济体国家,它希望对其中央银行关于利率变化的决定进行独立分析,这些决定是否影响了通货膨胀并让中央银行能够控制该变化。
以下是该国这些年平均利率和通货膨胀率的摘要。
以下是用于计算的数据。

该国总统已与您联系进行分析,并在下次会议上就此进行介绍。使用相关性并确定中央银行是否达到其目标。
解决方案:
使用上面讨论的公式,我们可以计算相关系数。将利率视为一个变量,例如x,将通货膨胀率视为另一个变量,y。

我们具有上表中的所有值,其中n = 6。
现在,输入用于计算相关系数的值。


r =(6 * 170.91)–(46.35 * 22.24)/√[(6 * 361.19)–(46.35)2] * [(6 * 82.74)–(22.24)2]
r = -5.36 / 5.88
相关将是–

相关性= -0.92
分析: 看来,利率与通货膨胀率之间的相关性为负,这似乎是正确的关系,因为利率上升时通货膨胀率下降,这意味着它们倾向于朝着相反的方向移动,从上面的结果看来,中央银行成功执行了有关利率政策的决定。
例子#3
ABC实验室正在研究身高和年龄,并想知道两者之间是否存在任何关系。他们针对每个类别收集了1000人的样本,并得出了该组中的平均身高。
以下是用于计算相关系数的数据。

您需要计算相关系数,并得出结论:是否存在任何关系。
解决方案:
将年龄作为一个变量,例如x,将身高(以厘米为单位)作为另一个变量,作为y。

我们具有上表中的所有值,其中n = 6。
现在,输入用于计算相关系数的值。


r =(6 * 10,137)–(70 * 850)/√[(6 * 940 –(70)2] * [(6 * 1,20,834)–(850)2]
r = 1,322.00 / 1,361.23
相关将是–

相关性= 0.971177099
相关性和用途
它在统计中主要用于分析所考虑变量之间关系的强度,并且还可以测量给定数据集之间是否存在线性关系以及它们之间的关联程度。关联中使用的常见度量之一是Pearson关联系数。
如果变量的值发生变化,并且该变量与其他变量的值一起发生变化,则理解这种关系至关重要,因为可以使用前一个变量的值来预测后一个变量的值的变化。如今,在当今的现代中,关联具有多种用途,就像它在金融业,科学研究中以及在其他地方所没有使用的那样。但是,重要的是要知道关联具有三种主要类型的关联。第一个是正向关系,它表示如果变量值发生变化,则相关变量在同一方向上也将发生变化,类似地,如果存在负向关系,则相关变量将在相反的方向。同样,如果没有相关性,则r表示零值。请参阅以下图像,以更好地理解该概念。