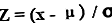Z得分公式| Z分数的逐步计算

计算Z分数的公式

原始数据的Z评分是指通过测量数据中总体平均值以上或以下多少个标准偏差而生成的得分，这有助于检验所考虑的假设。换句话说，数据点与总体平均值的距离表示为标准偏差的倍数。

z得分的变化范围是标准偏差的-3倍（正态分布的最左边）到标准偏差的+3倍（正态分布的最右边）。
Z分数的平均值为0，标准差为1。

通过从数据点中减去总体平均值来计算数据点的z分数方程（称为 X），然后将结果除以总体标准差。从数学上讲，它表示为

Z分数=（x – μ）/ ơ

在哪里

x =数据点
μ=平均值
ơ=标准偏差

Z分数的计算（逐步）

可以使用以下步骤来得出数据点的z分数公式：

步骤1： 首先，根据以x表示的数据点或观测值确定数据集的均值_一世，而数据集中的数据点总数用N表示。

第2步： 接下来，基于总体平均值μ，数据点x确定总体的标准偏差_一世以及总体N中的数据点数。

第三步： 最后，通过从数据点减去平均值得出z分数，然后将结果除以标准偏差，如下所示。

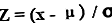
例子

您可以在此处下载此Z得分公式Excel模板– Z得分公式Excel模板

范例＃1

让我们以上周写过科学考试的50名学生为例。今天是考试的结果日，班主任告诉他，约翰在测试中得93分，而班上的平均分数是68分。如果标准差是13，请确定约翰的测试成绩的Z值。

解决方案：

鉴于，

约翰的考试成绩，x = 93
均值，μ= 68
标准偏差ơ= 13

因此，可以使用上面的公式来计算John的考试成绩的z得分，如下所示：

Z =（93 – 68）/ 13

Z分数将为–

Z分数= 1.92

因此，约翰的Ztest得分比全班平均得分高1.92个标准差，这意味着该班（49名学生）的97.26％得分低于约翰。

Example＃2

让我们再举一个详细的例子，其中有30名学生参加了班级测试（z检验不适用于少于30个数据点）。根据学生在100 – 55、67、84、65、59、68、77、95、88、78、53、81、73、66中获得的分数，确定第四名学生的z测验分数，65、52、54、83、86、94、85、72、62、64、74、82、58、57、51、91。

解决方案：

鉴于，

x = 65，
第四名学生得分= 65，
数据点数，N = 30。

均值=（55 + 67 + 84 + 65 + 59 + 68 + 77 + 95 + 88 + 78 + 53 + 81 + 73 + 66 + 65 + 52 + 54 + 83 + 86 + 94 + 85 + 72 + 62 + 64 + 74 + 82 + 58 + 57 + 51 + 91）/ 30

均值= 71.30

现在，可以使用如下所示的公式来计算标准偏差，

ơ= 13.44

因此，可以使用上述公式计算第四名学生的Z分数，如下所示：

Z =（x – x）/ s

Z =（65 –30）/ 13.44
Z = -0.47

因此，第四名学生的分数比班级的平均分数低0.47个标准差，这意味着，根据z得分表，班级（10名学生）中有31.92％的分数低于第四名学生。

Excel中的Z得分（带有Excel模板）

现在，让我们以示例2中提到的情况为例，说明下面的excel模板中z分数的概念。

以下是用于计算Z得分的数据

您可以参考以下给定的excel表格，详细了解Z得分公式测试统计信息。

photosdematures.com