photosdematures.com

Excel箱图

Excel中的箱形图 是用于表示数据集中数字分布的图形表示或图表。它指示数据集中的值如何散布。在箱图中，使用五个数字作为摘要显示了数值数据：最小值，最大值，第一四分位数，第二四分位数（中位数），第三四分位数。

在第一个四分位数和第三个四分位数之间，将绘制一个框，并沿着第二个四分位数绘制一条附加线以标记中位数。在第一和第三四分位数之外绘制了延长线，以描绘最小值和最大值。这些延长线在箱线图中称为晶须。

箱线图的框显示第一个到第三个四分位数，第二个四分位数处有一条线，即中位数。晶须的两端代表最小和最大。

箱形图表示的五个数字：

• 最低限度： 数据集的最小/最小值。
• 第一四分位数： 最小值和中位数的中间值。
• 第二四分位数/中位数： 数据集的中间值。
• 第三四分位数： 中值和最大值的中间值。
• 最大限度： 数据集的最大值。

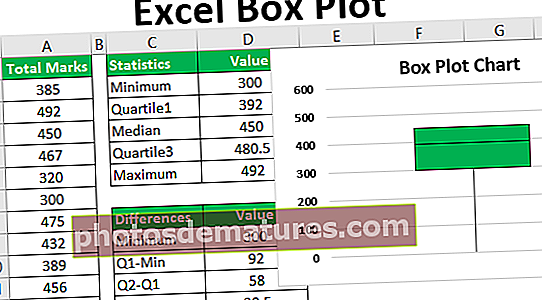
如何在Excel中制作方框图？ （带有示例）

假设我们有一个班级的数据集，其中包含其所有学科的学生总成绩（满分为500，满分：每个学科为100），并且我们希望在excel中创建一个箱形图。

我们在excel工作表中包含以下学生的评分数据：

现在，可以使用以下步骤为上述数据创建箱形图（基本上在excel 2013中）：

使用Excel 2016创建箱形图非常简单，因为默认情况下，它在统计图部分的统计图下有一个“箱体和晶须”图。但是，Excel 2013默认情况下没有用于箱形图的图表模板，因此我们必须按照以下步骤创建它：

通过使用以下函数，从数据集中计算箱形图所需的五个统计量：最小值，三个四分位数和最大值。

现在从数据集中计算最小统计量。

现在从数据集中计算分位数1统计信息。

计算箱形图的五个统计量将是–

现在，我们将创建一个最终表（例如差异表），该表将用于在excel中创建箱形图。在此最终表中，我们将复制最小值，这将是最终表的第一项。该最终表的其余条目将是各个统计之间的差异，如下所示：

现在，我们将使用该最终表创建一个堆叠的柱形图，并将其转换为箱形图。

因此，让我们首先在excel中创建一个堆积的柱形图：

选择差异和价值，然后点击“插入”->所有图表->堆积柱形图：

这样做后，我们得到一个堆积图，如下所示：

我们可以看到，这与箱形图并不相似，因为在此堆叠图表中，excel默认情况下是从水平而不是垂直数据集中绘制堆叠列。因此，我们将不得不反转图表轴。

为此，请在图表上单击鼠标右键，然后单击“选择数据”。

现在，点击“切换行/列”。

我们得到如下堆积图：

现在，我们将这种堆积图类型转换为箱形图，如下所示：

选择该列的底部（蓝色区域），然后单击“格式化数据系列”。

在“格式数据系列”面板中，展开“填充”选项，然后选择“无填充”按钮，然后从“边框”下拉菜单中，将其展开并选择“无行”按钮：

我们得到以下箱形图，如下所示：

下一步是通过用线条/晶须替换底部的最上面和第二个部分来创建晶须，即红色和橙色区域（因为我们已经删除了最底部的区域）。

要绘制顶部晶须，请选择最上方的区域/段（红色），然后展开“填充”标签。

然后选择“不填充”按钮。

现在，单击“设计”->“添加图表元素”->“错误栏”->“标准偏差”：

现在，我们单击图表右上方的加号按钮，然后选择并展开“ Excel中的错误栏”，然后选择“更多选项”。

这将打开“格式错误栏”面板并进行以下设置：

放： 指向“加号”的方向

结束样式为“上限”

占“ 100％”的百分比

因此，我们现在将绘制一个如下图所示的晶须：

类似地，绘制下部晶须，我们从底部区域中选择第二个晶须（橙色，现在可以看到最后一个），并重复与上述相同的步骤。唯一的变化是，错误栏中的“方向”将设置为“减”。

因此，我们现在将绘制出一个较低的晶须，如下所示：

因此，我们可以在上面的屏幕截图中看到，堆积的柱状图现在类似于箱形图。箱形图通常在整个颜色上都是相同的颜色，因此我们可以为其使用一种带有轻微边框的填充色。

现在让我们看看如何解释或查看箱形图：

我们可以在上面的屏幕截图中看到：

• 将晶须的端点降低至300，该端点表示最小值。
• 晶须的最高端点在500以下，恰好是492，代表了最大值。
• 绿色框的第一行描绘了四分位数3，我们看到的点为480.5。
• 绿框的中线表示中位数/四分位数2，我们看到的点是450。
• 绿色框的最后一行描绘了四分位数1，我们看到的点是392。

因此，正确地绘制了给定数据集的箱形图，并按上述方式计算了五个统计量（最小值，三个四分位数和最大值）。

要记住的事情

• 箱形图是数字数据集的图形表示，它使用五位数摘要来描述数据集的分布。
• 箱形图也称为箱形和晶须图。
• 它通常用于解释性数据分析。
• 当我们需要比较一些样本并测试数据是否对称分布时，通常使用它们。
• 与密度图或直方图相比，箱形图占用的空间更少。
• 它用于显示分布的形状，中心值及其可变性。
• 中间值不必在方框的中间。
• 晶须可以具有不同的长度。
• 箱形图可用于检测离群值。