photosdematures.com

有效利率定义

有效利率，也称为年度等效利率，是指个人在金融工具上实际支付或赚取的利率，该利率是通过考虑一段时间内的复利影响来计算的。

有效利率公式

有效利率公式=（1 + i / n）n –

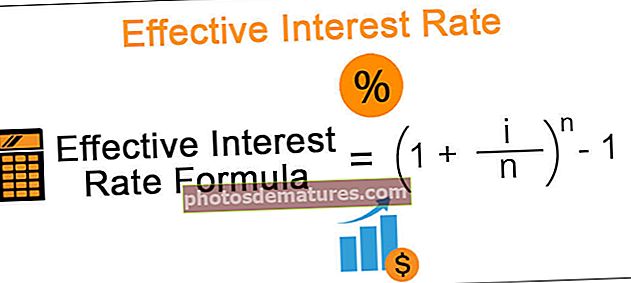
在这里，i =工具中提到的年利率。

n =表示每年的复利期数。

释义

复利改变利率。这就是为什么工具上写的利率对投资者而言不是有效利率（年等值利率）的原因。例如，如果工具上写有11％的利率，并且该利率每年复利四次，则年等值利率就不能为11％。

那会是什么呢？

应为–（1 + i / n）n – 1 =（1 + 0.11 / 4）4 – 1 = 1.1123 – 1 = 0.1123 = 11.23％。

这意味着11.23％是投资者的实际利率。

即使变化很小，也与工具中提到的年利率不同。

例子

Example＃1

婷买了一个特殊的乐器。票据上提到的利率为16％。他已经投资了大约100,000美元。该仪器每年复利。该特定工具的实际利率（AER）是多少？他每年将获得多少利息？

有效利率和年利率并不总是相同的，因为每年利息会多次复利。有时，利率每半年，每季度或每月复利一次。这就是年等值利率与年利率之间的差异。

本示例向您展示了这一点。

让我们计算一下。

由于利率逐年递增，因此这是有效的利率公式–

（1 + i / n）n – 1 =（1 + 0.16 / 1）1-1 = 1.16 – 1 = 0.16 = 16％。

这意味着在此特定示例中，年利率和等效年利率（AER）之间不会有差异。

每年，Ting都会从该工具获得=（$ 100,000 * 16％）= $ 16,000的利息。

Example＃2

堂买了一个特殊的乐器。票据上提到的利率为16％。他已经投资了大约100,000美元。该仪器每年复混六次。该特定工具的年等值汇率（AER）是多少？他每年将获得多少利息？

这只是前面示例的扩展。

但是有很大的不同。

在前面的示例中，该工具每年复利一次，这使得年利率类似于年等效利率。

但是，在这种情况下，情况完全不同。

在这里，我们得到的利率每年要复利六次。

因此，这是年利率的公式–

（1 + i / n）n – 1 =（1 + 0.16 / 6）6-1 = 1.171 – 1 = 0.171 = 17.1％。

现在，您可以看到，如果每年加息六次，那么年均等价率就会大不相同。

现在，由于有了有效利率，我们可以计算出Tong年底将获得的利息。

童将获得=（$ 100,000 * 17.1％）= $ 17,100。

如果我们将Ting在上一个示例中获得的利息与Tong在利率不同时获得的利息进行比较，我们将看到大约有1100美元的利息差。

Example＃3

平投资了一种乐器。她投资了10,000美元。该工具中提到的利率为18％。利息每月递增。了解第一年Ping如何每月获得利息。

这是年等效率的一个非常详细的示例。

在此示例中，我们将显示在不使用有效利率公式的情况下实际上如何进行计算。

我们来看一下。

由于利率按月复利，因此上述利率的实际每月违约=（18/12）= 1.5％。

• 在第一个月，Ping将获得=（10,000 * 1.5％）= $ 150的利息。
• 在第二个月，Ping将获得= {（（10,000 + 150）* 1.5％} =（10,150 * 1.5％）= 152.25美元的利息。
• 在第三个月，Ping将获得= {（（10,000 + 150 + 152.25）* 1.5％} =（10,302.25 * 1.5％）= 154.53美元的利息。
• 在第四个月，Ping将获得= {（10,000 + 150 + 152.25 + 154.53）* 1.5％} =（10,456.78 * 1.5％）= 156.85美元的利息。
• 在第五个月，Ping将获得= {（10,000 + 150 + 152.25 + 154.53 + 156.85）* 1.5％} =（10,613.63 * 1.5％）= 159.20美元的利息。
• 在第六个月，Ping将获得= {（10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20）* 1.5％} =（10,772.83 * 1.5％）= 161.59美元的利息。
• 在第七个月，Ping将获得= {（10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59）* 1.5％} =（10,934.42 * 1.5％）= 164.02美元的利息。
• 在第八个月，Ping将获得= {（10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02）* 1.5％} =（11098.44 * 1.5％）= 166.48美元的利息。
• 在第9个月，Ping将获得= {（10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48）* 1.5％} =（11264.92 * 1.5％）= 168.97美元的利息。
• 在第十个月，Ping将获得= {（10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97）* 1.5％} =（11433.89 * 1.5％）= 171.51美元的利息。
• 在第11个月，Ping将获得= {（10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51）* 1.5％} =（11605.40 * 1.5％）= 174.09美元。
• 在第12个月，Ping将获得= {（10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51 + 174.09）* 1.5％} =（11779.49 * 1.5％）= 176.69美元。

Ping一年获得的总利息为–

• (150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51 + 174.09 + 176.69) = $1956.18.

• 年度等效汇率公式=（1 + i / n）n – 1 =（1 + 0.18 / 12）12 – 1 = 1.195618 – 1 = 0.195618 = 19.5618％。

因此，Ping会收到的利息=（$ 10,000 ^ 19.5618％）= $ 1956.18。

Excel中的实际利率

为了在excel中找到有效利率或年等效率，我们使用excel函数效果。

• 标称利率是利率
• nper是每年的复利期数

让我们看下面的例子

• 如果您的名义利率为每年10％的复利，则年等效利率与10％相同。
• 如果您的名义利率是每六个月复利10％，那么年等效利率就等于10.25％。
• 如果您的名义利率是每季度复利10％，那么年等效利率就等于10.38％。
• 如果您的名义利率为每月复利的10％，则年等效利率为10.47％。
• 如果您的名义利率是每天复利的10％，则实际利率等于10.52％。

建议阅读

这是有效利率及其定义的指南。在这里，我们将讨论有效利率的公式以及逐步的计算方法。为了进一步学习，您可以参考以下文章

• 负利率示例
• 计算参与率
• 差异–贴现率与利率
• 名义利率公式
• 协整
<