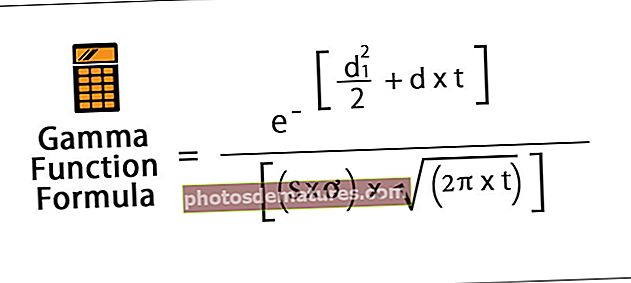photosdematures.com

在数学中，我们有指数，它是给定任何基数的幂，在excel中，我们有一个类似的内建函数，称为POWER函数，用于计算给定数或基数的幂，要使用此函数，我们可以关键字= POWER（在单元格中，并提供两个参数，一个作为数字，另一个作为幂。

在Excel中开机

Excel中的幂是数学/三角函数，用于计算并返回加到幂上的数字的结果。 Power Excel函数采用两个参数 底数（任何实数）， 和 指数（幂，表示给定数字将自身相乘多少次）。这意味着，例如5乘以2的幂等于5 x5。

幂函数公式

Excel中POWER功能的说明

Excel中的幂将两个参数都用作数值，因此传递的参数是整数类型，其中Number是基数，Power是指数。这两个参数都是必需的，不是可选的。

我们可以在Excel中以多种方式使用幂函数，例如用于数学运算，幂函数方程式，并且可以用于计算关系代数函数。

如何在Excel中使用POWER函数

Excel POWER功能非常简单易用。让我们通过一些示例来了解Excel中POWER的工作方式。

您可以在此处下载此POWER Function Excel模板– POWER Function Excel模板

Excel示例1中的POWER

例如，我们有一个幂函数方程y = x ^ n（x等于幂n），其中y取决于x的值，而n是指数。对于给定的x和n = 2的值，我们还想绘制此f（x，y）函数的图。 x的值为：

因此，在这种情况下，由于y的值取决于x的n次幂，因此我们将使用Excel中的POWER函数计算Y的值。

• y的第一个值将是2 ^ 2（= POWER（2,2）
• y的第二个值将是4 ^ 2（= POWER（4,2）
• ……………………………………………………………
• ……………………………………………………………
• y的第十个值将是10 ^ 2（= POWER（10,2）

现在，从范围B4：K5中选择x和y的值，然后从插入选项卡中选择图形（在此，我们选择了具有平滑线的散点图）。

因此，对于给定的POWER函数方程，我们得到了线性指数图。

Excel示例2中的POWER

在代数中，我们有二次幂函数方程，表示为ax2 + bx + c = 0，其中x是未知的，而a，b和c是系数。该幂函数方程的解给出了方程的根，即x的值。

二次幂函数方程的根是通过以下数学公式计算的

• x =（-b +（b2-4ac）1/2）/ 2a
• x =（-b-（b2-4ac）1/2）/ 2a

b2-4ac 被称为判别式，它描述了二次幂函数方程具有的根数。

现在，我们在A列中给出了二次幂函数方程的一些列表，我们需要找到方程的根。

^称为指数运算符，用于表示幂（指数）。 X2与x ^ 2相同。

我们有五个二次幂函数方程，我们将在excel中借助幂函数使用公式来求解它们，以找出根。

在第一个POWER函数方程中，a = 4，b = 56和c = -96，如果我们使用上述公式从数学上求解它们，则根为-15.5和1.5

要在excel公式中实现此功能，我们将在Excel中使用POWER函数，公式将为

• =（（-56 + POWER（POWER（56,2）-（4 * 4 *（-93）），1/2）））/（2 * 4） 将给出第一根，并
• =（（-56-电源（电源（56,2）-（4 * 4 *（-93）），1/2）））/（2 * 4） 将给出等式的第二个根

因此，完整的公式将是

=”方程的根是“＆”“＆（（-56 + POWER（POWER（56,2）-（4 * 4 *（-93）），1/2）））/（2 * 4）＆” ，“＆（（-56-POWER（POWER（56,2）-（4 * 4 *（-93）），1/2）））/（2 * 4）

这两个公式都与字符串“等式的根是”串联在一起。

对于其他的POWER函数方程，使用相同的公式，输出：

Excel示例3中的POWER

因此，对于不同的数学计算，我们可以在Excel中使用POWER函数。

假设我们必须找出公式为的复利

数量=本金（1 + r / n）nt

• 其中r是利率，n是每年复利的次数，t是时间
• 如果将$ 4000存入帐户（储蓄），年利率为5％，每月复利一次，则可以使用上述复利公式计算5年后的投资价值。
• 当本金= $ 4000，利率= 5/100即0.05，n = 12（按月计算），时间= 5年

使用复利公式并使用Excel中的POWER函数将其实现为excel公式，我们就有公式

= B2 *（电源（（1+（B3 / B5）），（B4 * B5）））

因此，五年后的投资余额为$ 5.133.43

Excel示例4中的POWER

根据牛顿的万有引力定律，两个重心之间的距离为r的物体根据引力POWER Excel公式在宇宙中相互吸引

F =（G * M * m）/ r2

其中F为重力大小，G为重力常数，M为第一个物体的质量，m为第二个物体的质量，r为两个物体之间距其重心的距离。

让我们计算一下太阳拉动地球的重力大小

• 太阳的质量是1.98 * 10 ^ 30公斤
• 地球质量为5.97 * 10 ^ 24公斤
• 太阳与地球之间的距离为1.496 x 10 ^ 11米
• 重力常数为6.67 * 10 ^ -11 m3kg-1s-2

在excel中，如果我们想计算重力，我们将再次使用Excel中的POWER，它可以对较大的数值进行运算。

• 因此，使用Excel中的POWER，我们可以将科学计数法值转换为POWER Excel公式
• 类似地，其他值也将以1.98 * 10 ^ 30表示为1.98 * Power（10,30）。
• 因此，用于计算力的POWER Excel公式将是=（6.67 *电源（10，-11）* 1.98 *电源（10,30）* 5.97 *电源（10,24））/电源（1.496 *电源（10,11），2）

由于作为力获得的值很大，因此Excel用科学的符号表示它。要将其更改为分数，请将格式更改为分数

输出：

因此，太阳以35229150283107900000000牛顿的力拉动地球。