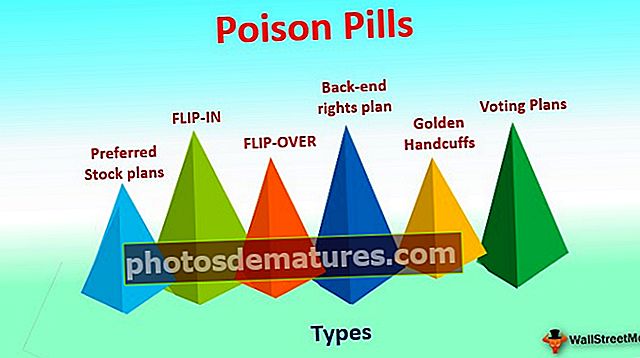
直方图示例直方图的前4个示例+说明
直方图图示例
直方图是用于汇总离散数据或连续数据的直观表示,其示例包括图形上的直观表示,银行针对不同参数在银行提出的客户投诉,在这些参数中,投诉的最多报告原因将是在显示的图形中具有最高的高度。
当使用各种高度的条形图以图形形式显示数据时,称为直方图。每个条形图都以直方图的形式分组。较高的条形图表示大多数数据将落在该较高的范围内。直方图描述了连续给定数据集或给定样本数据的散布和形状。在本文中,我们将为您提供直方图的前4个示例。

直方图的前4个示例
以下是直方图的前4个示例。
直方图示例#1
SBI经理Shaw先生担心客户抱怨分支机构排队太久。他想首先分析主要客户等待时间的频率。他已经叫了出纳员,并询问了细节。
以下是收银员观察到的高峰时段客户在SBI银行分行柜台的等待时间。您需要根据以下数据创建直方图。

解决方案:
我们使用5个具有5个不同频率的bin创建了直方图,如下图所示。在Y轴上,是属于该特定类别的平均客户数量。在X轴上,我们有等待时间的范围,例如,第一个bin范围是2.30分钟至2.86分钟。而且我们可以注意到,下表中该类别的计数为3,如下图所示。

这是一种随机分布,它是一种具有多个峰值并且缺乏明显模式的分布。
可能存在将各种数据属性组合在一起的情况。因此,应分别分析数据。
直方图示例2
著名的医生拉里(Larry)先生正在研究按8级标准学习的学生的身高。他收集了15名学生的样本,但想知道他们属于哪个类别。

解决方案:
我们创建了一个直方图,使用了6个具有6个不同频率的bin,如下图所示。在Y轴上,是属于该特定类别的平均学生人数。在X轴上,我们有高度范围,例如,第一个档位范围是138 cms至140 cms。我们可以注意到,该表中该类别的计数为1,如下图所示。

在这里,我们可以看到第八标准的学生平均身高在142厘米至146厘米之间。而且,可以注意到平均值的一侧也落在平均值的另一侧,这是正态分布的标志。
直方图示例#3
A先生想在股票市场上进行投资。他已经入围了低于库存的清单,并且想知道价格的频率。

使用直方图并说明这是哪种分布?
解决方案:
我们使用5个具有5个不同频率的bin创建了直方图,如下图所示。在Y轴上,是属于该特定类别的股票数量。在X轴上,我们有股价范围,例如,第一个仓位范围是100到300。从表中可以看出,该类别的计数是7,如下图所示。

在这里,我们可以注意到该图偏向左侧,因此这是分布的符号,它是右偏分布。大量的数据值出现在左侧,而较少的数据出现在右侧。
直方图示例#4
印度板球队的教练沙斯特里(Shastri)正在对板球运动员的平均得分进行分析,并希望为即将到来的世界杯确定最终的板球运动员。但是,他首先有兴趣创建一个基准来选拔击球手。在最近的15局比赛中,他已经收到了一个低于板球运动员的名单,但是,他想从这张名单中知道一个奇怪的人。使用直方图,找出一个出来,并对分布进行评论。

解决方案:
我们创建了一个直方图,使用了6个具有6个不同频率的bin,如下图所示。在Y轴上,是属于该特定类别的击球手的数量。在X轴上,我们具有游程范围,例如,第一个bin范围是90到190。并且我们可以注意到,该表中该类别的计数为1,如下图所示。

我们可以看到上表显示了一个左偏分布。大量的数据值出现在右侧,而较少的数据出现在左侧。
15局中有90局是奇数球,似乎是投球手,因此需要删除。
结论
创建直方图将提供给定数据集或数据分布的可视化表示形式。直方图显示数据值和大量数据的频率。直方图有助于确定给定数据集的中位数和分布。此外,这可以显示给定数据集中的任何缺口或异常值。