EWMA(指数加权移动平均线)|公式与范例
EWMA(指数加权移动平均线)的定义
指数加权移动平均线(EWMA)指的是数据的平均值,该数据用于通过检查结果和输出(通过考虑不同的因素并赋予其权重),然后跟踪结果以评估性能并跟踪结果来跟踪投资组合的移动。进行改进
EWMA的权重在过去的每个时期都以指数方式降低。同样,由于EWMA包含先前计算的平均值,因此指数加权移动平均值的结果将是累积的。因此,所有数据点都将对结果有所贡献,但是当计算下一个周期EWMA时,影响因子将降低。
解释
该EWMA公式显示了在时间t处的移动平均值。
EWMA(t)= a * x(t)+(1-a)* EWMA(t-1)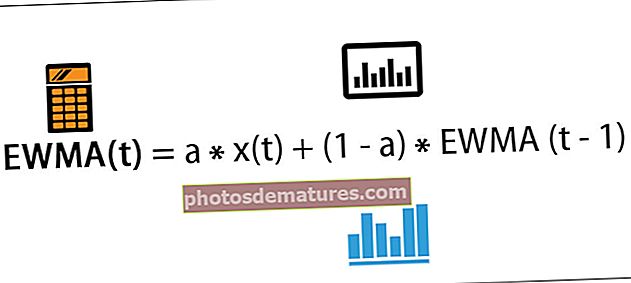
在哪里
- EWMA(t)=时间t的移动平均值
- a =介于0到1之间的混合度参数值
- x(t)=信号t在时间t的值
该公式表示在时间t处的移动平均线的值。这是一个参数,显示较旧数据的计算速率。 a的值将在0到1之间。
如果a = 1,则意味着仅使用最新数据来测量EWMA。如果a接近0,则意味着对较旧的数据赋予更大的权重;如果a接近1,则意味着对较新的数据赋予了更大的权重。
EWMA的示例
以下是指数加权移动平均线的示例
您可以在此处下载此EWMA Excel模板– EWMA Excel模板范例#1
让我们根据下表考虑5个数据点:

和参数 a = 30% 或0.3
因此EWMA(1)= 40
时间2的EWMA如下

- EWMA(2)= 0.3 * 45 +(1-0.3)* 40.00
- = 41.5
类似地,计算给定时间的指数加权移动平均值–

- EWMA(3)= 0.3 * 43 +(1-0.3)* 41.5 = 41.95
- EWMA(4)= 0.3 * 31 +(1-0.3)* 41.95 = 38.67
- EWMA(5)= 0.3 * 20 +(1-0.3)* 38.67 = 33.07
范例#2
从星期日到星期六,我们的气温处于摄氏温度。使用= 10%,我们将得出一周中每一天的温度移动平均值。

使用 a = 10% 我们将在下表中找到每天的指数加权移动平均值:

下图显示了实际温度与EWMA之间的比较:

如我们所见,使用= 10%进行平滑非常强大。我们可以用相同的方法来求解多种时间序列或顺序数据集的指数加权移动平均值。
好处
- 这可用于使用整个数据或输出历史记录来查找平均值。所有其他图表都倾向于以单独的方式处理每个数据。
- 用户可以根据自己的方便性对每个数据点进行加权。可以更改此权重以比较各种平均值。
- EWMA以几何方式显示数据。因此,发生异常值时数据不会受到太大影响。
- 指数加权移动平均值中的每个数据点都代表点的移动平均值。
局限性
- 仅当可获得一段时间内的连续数据时,才可以使用此功能。
- 仅当我们要检测过程中的微小变化时,才可以使用此方法。
- 此方法可用于计算平均值。监视方差要求用户使用其他技术。
重要事项
- 我们要获取指数加权移动平均值的数据应按时间排序。
- 这对于减少嘈杂的时间序列数据点(可以称为平滑)中的噪声非常有帮助。
- 每个输出都有权重。最新的数据是权重最高。
- 它在检测较小的偏移方面相当不错,但在检测较大的偏移方面比较慢。
- 当子组样本大小大于1时,可以使用它。
- 在现实世界中,此方法可用于化学过程和日常会计过程。
- 它也可以用于显示网站访问者在一周中的每一天的波动。
结论
EWMA是一种用于检测时间限制过程中较小偏差的工具。指数加权移动平均值也得到了高度研究,并使用模型来查找数据的移动平均值。在预测过去数据的事件基础时,它也非常有用。指数加权移动平均线是观测值呈正态分布的假定基础。它正在根据其权重考虑过去的数据。由于过去的数据更多,因此其计算权重将呈指数下降。
用户还可以对过去的数据进行加权,以根据不同的权重找到不同的EWMA集。另外,由于数据显示的是几何图形,因此离群值对数据的影响也不大,因此使用此方法可以实现更平滑的数据。