photosdematures.com

夏普比率定义

夏普比率 是William F. Sharpe开发的比率，供投资者用来得出投资组合的波动率（标准差）的无风险收益率之上的投资组合的平均收益率。

解释

夏普比率是衡量投资组合整体收益的关键组成部分。它是所赚取的平均收益超过无风险收益与承担的风险总额之和。这是一种通过调整风险成分来检查投资绩效的方法。夏普比率表征了资产收益补偿投资者承担的风险的程度。当将两种资产与共同基准进行比较时，具有较高夏普比率的资产被表示为在相同风险水平下的有利投资机会。

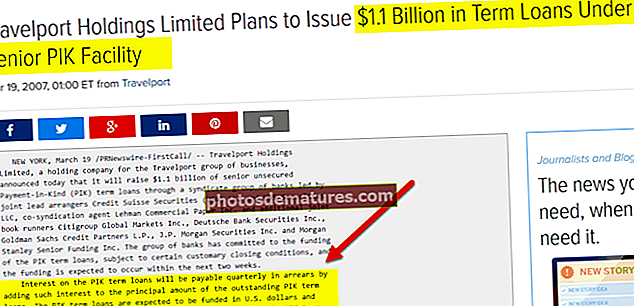
如果您查看上表，您会发现PRWCX的夏普比率更高，为1.48，是该类别中最好的基金。

像任何其他数学模型一样，夏普比率依赖于需要正确的数据准确性。在通过收益平滑化检查资产的投资绩效时，夏普比率将从基础资产的绩效中获得，而不是从基金收益中得出。该比率以及Treynor比率和Jeson的Alpha经常用于对各种投资组合或基金经理的业绩进行排名。

公式

1966年，威廉·夏普（William Sharpe）开发了该比率，该比率最初被称为“收益-可变性”比率，随后被后来的学者和金融运营商称为“夏普比率”。它以多种方式定义，直到最终如下图所示：

夏普比率公式=（预期收益–无风险收益率）/标准差（波动率）

我们需要理解的一些概念是：

• 退货 –只要可以正常分布分布，收益就可以有不同的频率，例如每天，每周，每月或每年，因为这些收益可以被年度化以得出精确的结果。诸如较高的峰，分布的偏度之类的异常情况可能是比率的问题区域，因为当存在这些问题时标准偏差不具有相同的有效性。
• 无风险收益率– 这用于评估由于该风险资产而为他人所承担的额外风险是否得到了正确的补偿。传统上，没有财务损失的回报率是期限最短的政府证券（例如美国国库券）。尽管此类证券的波动性最小，但可以认为此类证券应与期限相同的其他证券匹配。
• 标准偏差– 它是一个数量，表示给定变量集中有多少个单位与该组的平均数不同。一旦计算出超出无风险收益的超额收益，就必须将其除以要衡量的风险资产的标准差。从风险/回报的角度来看，数量越多，投资将越有吸引力。但是，除非标准偏差很大，否则杠杆成分可能不会影响该比率。分子（返回）和分母（标准偏差）都可以加倍而没有问题。

例子

客户“ A”目前持有$ 450,000的投资组合，预期收益为12％，波幅为10％。高效的投资组合的预期回报率为17％，波幅为12％。无风险利率为5％。什么是夏普比率？

夏普比率公式=（预期收益–无风险收益率）/标准差（波动率）

夏普比率=（0.12-0.05）/0.10 = 70％或0.7x

在Excel中计算Sharpe比率

现在我们知道了公式的工作原理，让我们计算excel中的Sharpe Ratio。

步骤1 –以表格形式获取退货

第一步涉及安排要分析的共同基金投资组合的回报。时间段可以是每月，每季度或每年。下表提供了共同基金的年收益。

步骤2 –在表格中获取无风险退货明细

在下表中，我假设15年的无风险收益为3.0％。但是，无风险利率可能每年都会变化，您需要在此输入该数字。

步骤3 –查找超额退货

计算Excel中的Sharpe比率的第三步是找到投资组合的超额收益。在我们的案例中，超额收益是“年度收益–无风险收益”。

第4步–计算年报的平均值。

计算excel中Sharpe比率的第四步是找到年收益的平均值。您可以使用excel公式AVERAGE查找投资组合的平均值。在我们的示例中，我们获得了12.09％的平均回报。

步骤5 –查找超额收益的标准偏差

为了找到超额收益的标准差，您可以使用下面给出的excel公式STDEV。

步骤6 –计算夏普比率

计算excel中Sharpe比率的最后一步是将平均收益除以标准差。我们得到的比例= 12.09％/ 8.8％= 1.37x

我们得到的比例= 12.09％/ 8.8％= 1.37x

使用夏普比率的优点

＃1 –夏普比率有助于比较和对比新资产

每当将新资产或一类资产添加到投资组合时，就可以用来比较投资组合的整体风险收益特征的方差。

• 例如，一个投资组合经理正在考虑向夏普比率为0.81的他现有的80/20股票投资组合中增加商品基金的分配。
• 如果新投资组合的分配是40/40/20股票，债券和债务基金分配，则夏普比率将提高到0.92。

这表明，尽管大宗商品基金投资作为独立敞口波动较大，但在这种情况下，它实际上导致了组合投资组合的风险收益特征的改善，从而增加了分散投资至另一项资产的好处。分类到现有的投资组合。必须进行仔细的分析，如果资金分配对投资组合的健康产生负面影响，则可能必须在稍后阶段更改资金分配。如果增加新投资导致比率下降，则不应将其包括在投资组合中。

＃2 –夏普比率有助于风险回报比较

该比率还可以为投资组合的超额收益是由于谨慎的投资决策还是由于过度承担风险而提供的指导。尽管单个基金或投资组合享有的收益要高于同类基金，但如果这些较高的收益不会带来不适当的风险，那只是一种合理的投资。资产组合的夏普比率越大，其风险因素的表现就越好。夏普比率为负表示较低风险的资产将比所分析的证券表现更好。

让我们以风险收益比较为例。

假设投资组合A具有或预期具有12％的收益率，标准差为0.15。假设基准回报率为1.5％，则回报率（R）为0.12，Rf为0.015，“ s”为0.15。该比率将被读取为（0.12-0.015）/0.15，计算得出为0.70。不过，将这个数字与另一个投资组合（例如投资组合“ B”）进行比较会很有意义

如果投资组合“ B”比投资组合“ A”显示出更大的可变性，但具有相同的收益，则在具有相同收益率的情况下，其标准差将更大。假设投资组合B的标准偏差为0.20，则该等式应理解为（0.12 – 0.015）/ 0.15。该投资组合的夏普比率为0.53，比投资组合“ A”低。考虑到两个投资都提供相同的回报，但这并不是一个令人惊讶的结果，但是“ B”具有更大的风险范围。显然，风险较小，提供相同回报的人将是首选。

对夏普比率的批评

夏普比率使用分母中收益的标准偏差作为总投资组合风险的替代方法，并假设收益是平均分配的。过去的测试表明，某些金融资产的回报可能会偏离正态分布，从而导致对Sharpe比率的相关解释具有误导性。

可以通过各种基金管理人试图提高其表观风险调整后的收益来提高该比率，可以如下执行：

1. 增加要测量的持续时间：这将导致波动的可能性较小。例如，每日收益的年度标准差通常高于每周收益，而每周收益又高于每月收益。持续时间越长，图片越清晰，就必须排除可能影响整体性能的一次性因素。
2. 每月收益的复利 但要计算标准差（不包括最近计算出的复合月收益）。
3. 编写投资组合的平价卖出和买入决定： 这样的策略可以通过收取期权费而不用多年的回报来潜在地增加回报。涉及挑战违约风险，流动性风险或其他形式的广泛分散风险的策略，具有相同的能力来报告较高的夏普比率。
4. 收益的平滑化： 使用某些衍生产品结构，对流动性较低的资产进行不规则标记或使用某些低估每月损益的定价模型，可以减少预期的波动性。
5. 消除极端收益： 回报率过高或过低都会增加任何投资组合的报告标准偏差，因为这是与平均值的距离。在这种情况下，基金经理可能会选择消除每年的极端（最佳和最差）月收益率，以减少标准差并影响结果，因为这种一次性情况会影响总体平均值。

事前和事后夏普比率

夏普比率已被多次修订，但使用了两种一般形式：事前（对未来收益和方差的预测）和事后（对过去收益方差的分析）。

• 事前夏普比率 预测很容易 估计模式 在观察过类似投资活动的过去表现之后。
• 事后夏普比率 衡量收益的高低，以及这些收益在给定时间段内的变化程度。更具体地说，它是差异收益（投资收益与基准投资之间的差异）与这些收益的历史变异性（标准差）之比。

结论

夏普比率是衡量投资组合绩效的标准指标。由于其简单和易于解释，它是最受欢迎的索引之一。不幸的是，大多数用户忘记了导致不合适结果的假设。在做出市场决策之前，您应该考虑检查收益的分布或使用等效的绩效指标对结果进行验证。