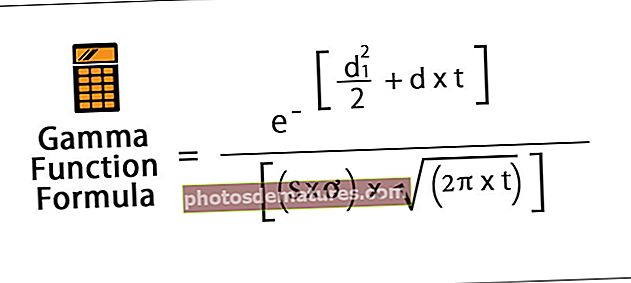photosdematures.com

什么是有效利息法？

有效利率法是在金融工具的整个存续期间内，利用标准利率和金融工具的市场利率来分配利息支出，以达到通过折价或溢价出售而累积的工具的面值的目的。利息支出分别在系统和一致的基础上摊销至金融工具的账面价值。

当市场利率高于票面利率时，债券债券将以折扣价出售，因为买方愿意支付比债券市场价格低的价格。当市场利率低于票面利率时，债券债券将溢价出售。在理想情况下，票面利率与市场利率完全匹配，意味着债券以面值发行。

有效利率法公式

有效利息法的计算公式如下：

在哪里，

i =利率（票息率），n =每年的期数。如果利息每半年支付一次，则年份应除以2。

实际利率法的例子

以下是计算实际利率法的示例–

您可以在此处下载此有效利率法Excel模板–有效利率法Excel模板

例1 –以折扣价发行的债券/债券

以折扣价发行的金融工具意味着买方支付的价格低于该金融工具的票面价值。在这种情况下，支付的金额与债券的账面价值之间的差额是折扣，并在债券的存续期内摊销。每个金融工具都带有一个利率，该利率被称为每年付息一次，每半年支付给债券持有人。

付息票/利息与摊销折价之间的差额是债券价值的增加。到期时，债券的账面价值将达到债券的票面价值，并支付给债券持有人。假设在1月17日以10％的市场$ 96,149发行了9％的半年期票息的100,000美元的5年期债券，并在6月和1月支付了利息。

解决方案

利息支付的计算

• =100000*4.5%
• =4500

利息费用的计算

差异将如下所示–

折价发行债券的会计分录

每年都会通过类似的条目。债券到期时，A / c将记入借方，银行A / c将记入100,000美元。

例2 –溢价发行的债券/债券

以溢价发行的金融工具意味着买方支付的价值比金融工具的面值多。在这种情况下，支付的金额与债券的账面价值之间的差额是溢价，并在债券的存续期内摊销。每个金融工具都带有利率，该利率被称为每年付息一次，每半年付给债券持有人。

已付息票/利息与摊销的溢价之间的差额是按债券的价值摊销。到期时，债券的账面价值将达到债券的面值，并支付给债券持有人。假设在1月17日以8％的市场108,530美元发行了6％的半年期票息为100,000美元的5年期债券，并在6月和1月支付了利息。

解决方案

利息支付的计算

利息费用的计算

差异将如下所示–

溢价发行债券的会计分录

每年都会通过类似的条目。债券到期时，A / c将记入借方，银行A / c将记入100,000美元。

例3 –以面值发行的债券/债券

按面值发行的金融工具意味着买方已为金融工具支付了准确的价值。在这种情况下，票面利率等于市场利率。由于债券的账面价值恰好等于债券的票面价值，因此不适用实际利率法。普通日记帐分录将在债券发行，应计，利息支付，到期本金支付时通过。

有效利率法的实际应用

• 以折扣价和溢价发行的债券/债券。
• 根据国际财务报告准则计算保证金的现值。
• 计算租赁安排下的最低租赁付款额的现值。

好处

• 没有突然的损益表或收入到损益表。折价和溢价分散在债券的存续期内。
• 此方法中使用了更好的会计惯例，例如匹配概念
• 提前知道对损益表的未来影响，这有助于制定更准确的利息支出预算。

缺点

• 一种方法比直线摊销方法更复杂。
• 不适用于折旧会计。

结论

基于以上讨论，我们可以得出结论，实际利率法是计算利息支出的一种比其他方法更为准确的方法。尽管实际利率法有一定的局限性，但这种方法显然遵循了匹配概念之类的会计概念。