均值与中位数|统计中使用的方法之间的差异
中位数和中位数之间的差异
中位数和中位数 是数学中的两个常用术语,均值就像给定数字的平均值,将它们相加并除以数字计数即可得出平均值,而中位数则从整个数据集中返回中间数,如果数据集是偶数,则中位数将两个中间数字相加并除以2,得到中位数。
它们是集中趋势的度量,通常用于测量需要绘制分析和解释结果的大型数据集。平均值,中位数和众数是平均值的三个度量,显示数据来自平均值或平均值的离散度。这些方法广泛用于统计中,而数据的平均值是这三种方法中使用最广泛的方法。
什么意思
平均值是阵列中观察值的简单总和,然后除以观察值。例如,如果我们谈论由5个人组成的组的平均身高或平均身高。平均身高的计算方法是将5个人的身高除以人数即5。
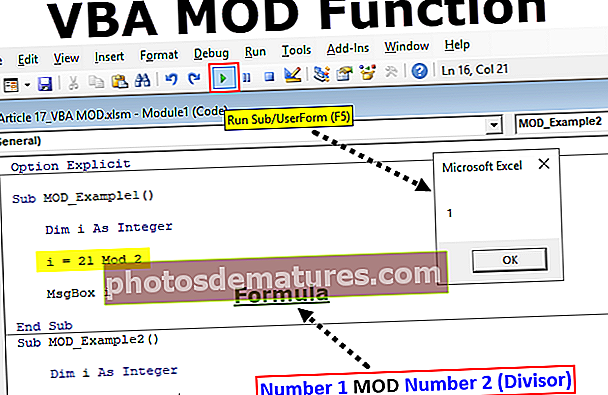
公式
平均值=(所有观测值的总和/观测值的数量)
中位数是多少?
另一方面,中位数是数据数组集中的中间数字,该中间数字将较高的数据集与较低的数据集分开。首先需要按升序排列数据,以计算数据的中位数。当数据集具有基数时,需要获取数据集中的中间两个数字的平均值。但是,这两种方法经常互换使用。
公式
中值公式 =(n + 1)/ 2当n是奇数时
中位数= [(n / 2)+ {(n / 2)+1}] / 2当n是偶数时
平均值与中位数信息图表
让我们来看看平均值与中位数之间的最大差异。

均值与中位数关键差异
- Mean易于使用和应用,并且可以应用于任何数据数组,无论是偶数还是奇数。另一方面,中位数的使用有点复杂,在计算之前,数据集需要先按升序或降序排列。
- 平均值通常用于正态分布,而中位数用于偏斜分布数据集。
- 平均值很简单,但并不稳健,因为它可能包含分布中的异常值,有时无法为用户提供正确的解释结果。另一方面,中位数方法是健壮的,并且更适合用于偏斜分布以得出日期集的集中趋势,并且与均值相比将为用户提供许多准确的结果
- 平均值只有一个公式,即所有观测值的总和除以观测值的数量。而中位数有两个公式之一,即奇数,只有数据集中的中间数成为中位数。但是,当我们拥有偶数数据集时,将选择两个值的中间值并将它们除以2,这将为我们提供偶数数据集的中值。
平均值与中位数比较表
| 意思是 | 中位数 | |
| 通过将数据数组中的所有值相加得出平均值,然后除以观察数 | 中位数是数据集的确切中间值。可以通过按升序排列数据集,然后从数据集中查找或挑选出中间值来进行计算 | |
| 由于易于计算平均值,因此在行业中得到了更广泛的应用,它为我们提供了一个快速的数字 | 它在行业中并不经常使用,但是比简单的数字总和要更完整和准确 | |
| 它通常用于正常偏斜的数据集,即正态分布 | 在数据中存在明显偏斜或数据尾巴较长时,描述数据集特别方便。它被广泛使用,其中轮廓绘制器在数据中占很大的比重,这意味着不是一个好的计算方法 | |
| 它不是用于计算集中趋势的可靠工具 | 这是一个非常强大的工具,因为它可以确定数据中的权重,通常在较长的尾巴上权重较高 | |
| 对异常值非常敏感 | 它受异常值的影响要小得多 | |
| 使用简单 | 本质上很复杂 | |
| 无法对分类数据进行计算,因为无法对这些值求和 | 由于无法对其进行逻辑排序,因此无法将其标识为分类的名义数据。 |
结论
除了均值和中位数,还有另一种方法通常用于测量中心趋势即众数。众数是最常出现在数据集中的一个值,该模式具有优于均值和中位数的优势,可以在数值和分类数据集中找到它。
尽管存在众数和中位数,但均值仍是更好的结果和分析方法的优势,但均值仍然是集中趋势的最合适度量,尤其是在数据集为正态分布且数据通常为偏斜的情况下。
作为一名优秀的分析师,应使用所有三种数据方法来衡量中心趋势,并应考虑和仔细分析分析中的差异,以在数据集中产生更好,更准确的结果。