photosdematures.com

确定总体样本量的公式

样本数量公式有助于计算或确定所需的最小样本数量，以便了解总体的适当或正确比例以及置信度水平和误差范围。

术语“样本”是指能够使我们得出有关种群的推论的总体部分，因此重要的是，样本量要足够大，以便可以做出有意义的推论。换句话说，这是估计实际人口比例以及所需的误差范围和置信度所需的最小尺寸。因此，确定合适的样本量是统计分析中经常出现的问题之一。它的方程式可以通过使用总体大小，正态分布的临界值，样本比例和误差幅度来得出。

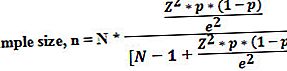
在哪里，

• N =人口规模，
• Z =在所需置信度下的正态分布的临界值，
• p =样本比例
• e =误差幅度

如何计算样本量？ （一步步）

• 步骤1： 首先，确定人口规模，即人口中不同实体的总数，并用N表示。对于大于此的人口，大小没有太大变化。]
• 第2步： 接下来，在所需的置信度下确定正态分布的临界值。例如，在95％置信度下的临界值为1.96。
• 第三步： 接下来，确定可以从以前的调查结果中使用的样本比例，或者通过运行小型试点调查来收集样本比例。 [注意：如果不确定，总是可以使用0.5作为保守方法，这将提供最大的样本量。]
• 第4步： 接下来，确定误差范围，该范围是预期真实人口所处的范围. [注意：误差范围越小，精度越高，因此准确答案也就越多。]
• 步骤5： 最后，可以通过使用总体大小（步骤1），在所需置信度下的正态分布的临界值（步骤2），样本比例（步骤3）和误差幅度（步骤4）得出样本大小方程式。如下所示。

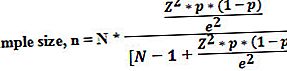
例子

范例＃1

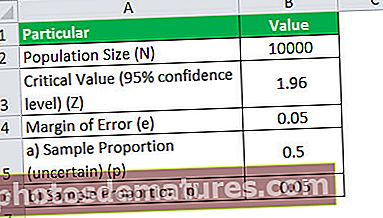
让我们以一个零售商为例，该零售商有兴趣在一天中查看他们的网站后知道有多少客户从他们那里购买了商品。假设他们的网站平均每天有10,000次访问，请确定在以下情况下他们必须以95％的置信度和5％的误差幅度监视的客户样本量：

• 他们不确定当前的转换率。
• 他们从以前的调查中知道转换率是5％。

鉴于，

• 人口总数，N = 10,000
• 95％置信水平下的临界值，Z = 1.96
• 误差范围，e = 5％或0.05

1 –由于当前的转换率未知，因此让我们假设p = 0.5

因此，可以使用以下公式计算样本量：

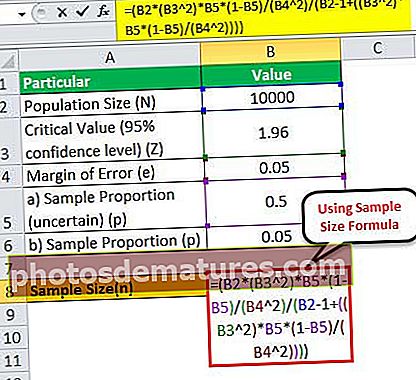
= (10,000 * (1.96 2)*0.5*(1-0.5)/(0.05 2)/(10000 – 1+((1.96 2)* 0.5*(1-0.5)/(0.05 2))))

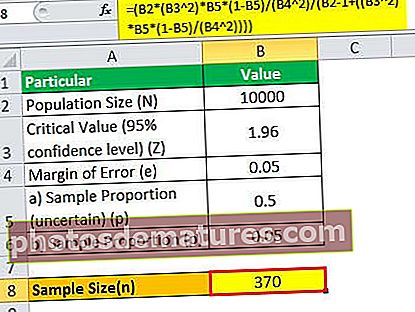
因此，有370个客户将足以得出有意义的推论。

2 –当前的转换率是p = 5％或0.05

因此，可以使用上述公式计算样本量，如下所示：

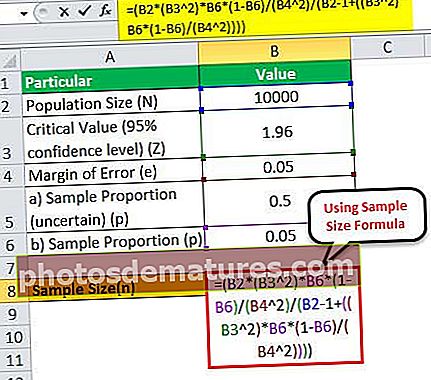
= (10,000 * (1.96 2)*0.05*(1-0.05)/(0.05 2)/(10000 – 1+((1.96 2)* 0.05*(1-0.05)/(0.05 2))))

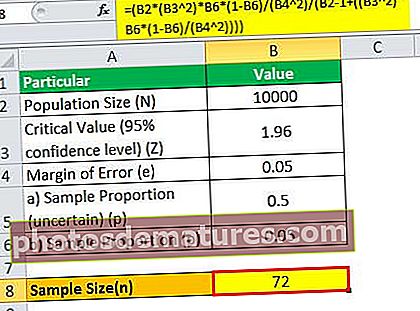
因此，在这种情况下，有72位客户就足够进行有意义的推断。

范例＃2

让我们以上面的示例为例，在这种情况下，我们假设人口规模（即每日网站浏览量）在100,000和120,000之间，但是不知道确切值。其余值相同，转化率均为5％。计算100,000和120,000的样本量。

鉴于，

• 样本比例，p = 0.05
• 95％置信水平下的临界值，Z = 1.96
• 误差幅度，e = 0.05

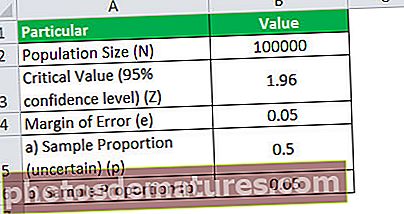
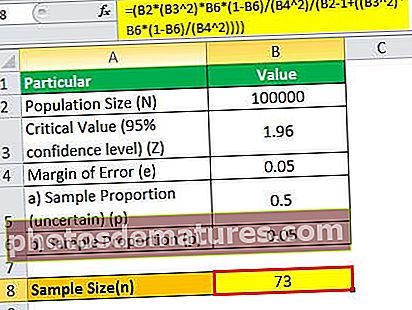
因此，N = 100,000的样本量可以计算为：

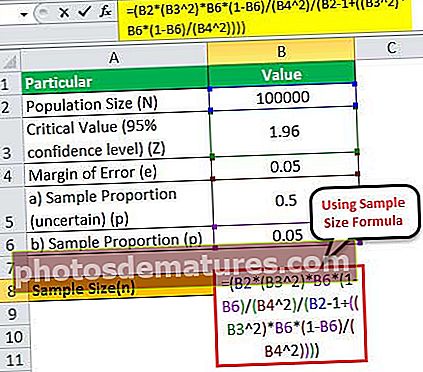
= (100000 * (1.96 2)*0.05*(1-0.05)/(0.05 2)/(100000 – 1+((1.96 2)* 0.05*(1-0.05)/(0.05 2))))

因此，N = 120,000的样本量可以计算为：

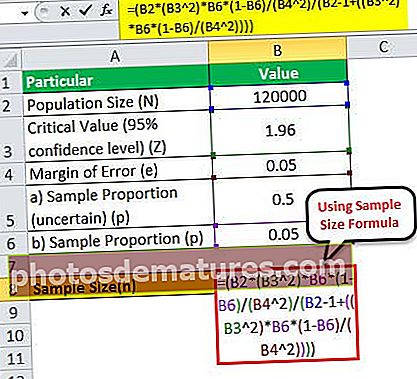
= (120000 * (1.96 2)*0.05*(1-0.05)/(0.05 2)/(120000 – 1+((1.96 2)* 0.05*(1-0.05)/(0.05 2))))

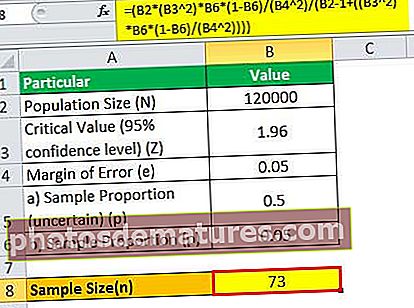
因此，证明了随着人口规模的增加而变得非常大，在样本量的计算中变得无关紧要。

相关性和用途

样本量计算对于理解适当样本量的概念很重要，因为它用于研究结果的有效性。如果样本太小，则不会产生有效的结果，而样本太大，可能会浪费金钱和时间。从统计上讲，大量样本主要用于市场研究调查，医疗保健调查和教育调查。