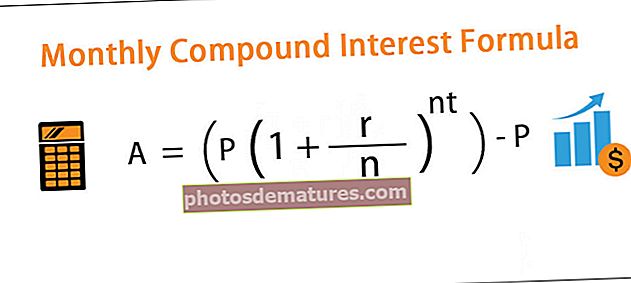photosdematures.com

什么是有效年利率（EAR）？

有效年利率（EAR）是在给定时间段内进行复利后在投资中实际赚取或对贷款支付的利率，用于比较不同复利期（即每周，每月，每年等）的金融产品。增加，EAR增加。

公式

EAR计算如下：

有效年利率=（1 + i / n）n – 1

• 其中n =复利期数
• i =名义利率或给定的年利率

仅当每年进行复利时，EAR才等于名义利率。随着复利期数的增加，EAR也随之增加。如果是连续复配公式，则EAR如下：

有效年利率（在连续复利的情况下）= ei –

因此，有效年利率的计算取决于两个因素：

• 名义利率
• 复利期数

随着EAR随着期数的增加，复利期数是主要因素。

如何计算？

范例＃1

让我们考虑以下示例：

考虑名义利率为12％。让我们计算每年，半年，季度，每月，每月，每周，每天和连续进行复利时的有效年利率。

年度复利：

• EAR =（1 + 12％/ 1）1 – 1 = 12％

半–年度复利：

• EAR =（1 + 12％/ 2）2 – 1 = 12.36％

季度复利：

• EAR =（1 + 12％/ 4）4 – 1 = 12.55％

每月复利：

• EAR =（1 + 12％/ 12）12 – 1 = 12.68％

每周复利：

• EAR =（1 + 12％/ 52）52 – 1 = 12.73％

每日复利：

• EAR =（1 + 12％/ 365）365 – 1 = 12.747％

连续复配：

• EAR = e12％– 1 = 12.749％

因此，从上面的示例可以看出，连续计算有效年率的计算最高，而每年进行复利时的计算则最低。

范例＃2

在比较两个不同的投资时，计算很重要。让我们考虑以下情况。

投资者有10,000美元，他可以投资于半年度复合年利率为10％的金融工具A，也可以投资于月度复合年利率为8％的金融工具B。我们需要找到哪种金融工具更适合投资者，为什么？

为了找到哪种工具更好，我们应该找到他在每项投资一年后将获得的金额：

投资一年后的金额 = P *（1 + i / n）n

其中P是本金，I是名义利率，n是复利的周​​期数，在这种情况下为2

• 因此，一年后的投资额A = 10000 *（1 + 10％/ 2）2 A = $ 11025

投资一年后的金额 = P *（1 + i / n）n

其中P是本金，I是名义利率，n是复利的周​​期数，在这种情况下为12

• 因此，一年后投资的金额A = 10000 *（1 + 8％/ 12）12 = B = $ 10830

因此，在这种情况下，对于投资者而言，投资A是更好的选择，因为一年后赚取的金额更多地来自投资A。

如果将利息复利，则会在随后的期间产生较高的利息，最高的是在最后一个期间。到目前为止，我们已经考虑了年底的总金额。

例子＃3

让我们看下面的例子，在每个周期结束时找到兴趣。

一种金融工具的初始投资为5000美元，每季度复合年利率为15％。让我们计算投资获得的季度利息。

该利率按季度复利，因此每个季度的利率= 15％/ 4 = 3.75％

第一季度赚取的利息= P（1 + i / n）n – P = 5000 *（1 + 15％/ 4）– 5000 = $ 187.5

• 现在，新的本金是5000 + 187.5 = $ 5187.5

因此，第二季度赚取的利息= P（1 + i / n）n – P = 5187.5 *（1 + 15％/ 4）– 5187.5 = $ 194.53

• 现在，新的本金是5187.5+ 194.53 = $ 5382.03

因此，第三季度赚取的利息= P（1 + i / n）n – P = 5382.03 *（1 + 15％/ 4）– 5382.03 = $ 201.82

• 现在，新的本金是5382.03+ 201.82 = $ 5583.85

因此，第四季度赚取的利息= P（1 + i / n）n – P = 5583.85 *（1 + 15％/ 4）– 5583.85 = $ 209.39

• 因此，一年后的最终金额将为5583.85 + 209.39 = $ 5793.25

从上面的示例可以看出，第四季度所赚取的利息是最高的。

结论

有效年利率是投资者从其投资中赚取的实际利率或借款人向贷方支付的实际利率。它取决于复利期数和名义利率。如果以相同的名义利率增加复利期数，则EAR会增加，如果连续进行复利，则EAR最高。