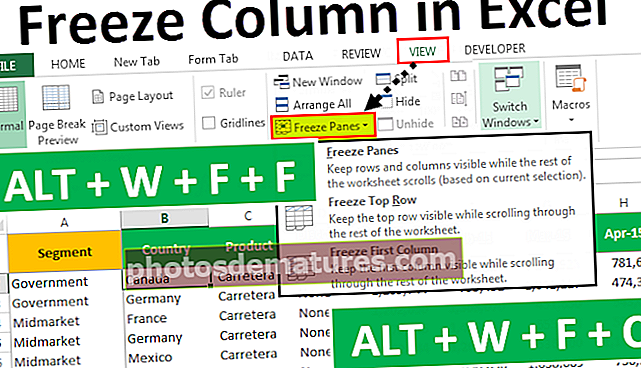
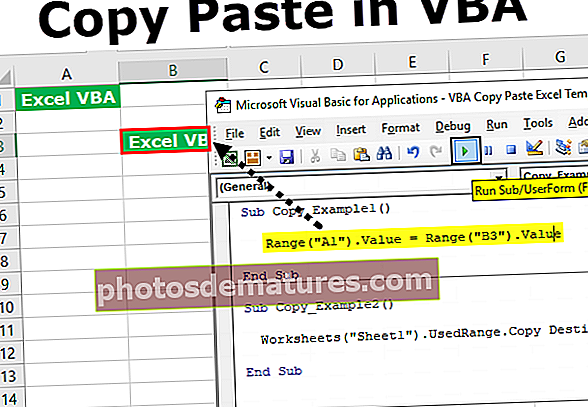
方差与标准偏差|前6个差异(信息图形)
方差和标准偏差之间的差异
方差 是一种在变量之间找到或获得度量的方法,它们之间有何不同? 标准偏差 向我们展示了数据集或变量与数据集的平均值或平均值有何不同。
方差有助于从均值中找到总体中的数据分布,而标准偏差也有助于了解总体中的数据分布,但是标准偏差可以使数据与均值之间的偏差更加清晰。

公式
以下是方差和标准偏差的公式。

然而
- σ2是方差
- X是可变的
- μ是平均值
- N是变量的总数。
标准偏差是方差的平方根。
例子
想象一个像这样的游戏
情况1
您从普通纸牌中抽出一张纸牌
- 如果您抽奖7,您将赢得2000印度卢比/-
- 如果您选择除7以外的其他卡,则将获得100印度卢比/-

案例2
- 如果您抽奖7,您将赢得1,22,000印度卢比/-
- 如果您选择除7以外的其他卡,则将获得10,100印度卢比/-
假设您玩了52,000次游戏。

对于离散随机变量,方差为

其中Pi是结果的概率。
在这两种情况下,每款游戏的平均利润为Rs.61.54,您希望哪种游戏表现出色,有某种工具可以帮助您做出决策,即我们必须计算方差和标准差

我们需要测量与期望值的正态偏差,一种常见的测量方法是方差。案例-1的方差远小于案例-2的方差,这意味着案例-2的数据传播平均值,即64.54卢比,因此案例1的博弈风险小于案例2的博弈。
在金融领域,我们谈到了股票的波动性,这意味着金融资产收益率的大冲击往往伴随着大冲击,而金融资产收益率的小冲击往往伴随着小冲击。
方差与标准偏差图表
让我们来看看方差与标准偏差之间的最大差异。

关键差异
主要区别如下:
- 方差给出了数据波动性的近似概念。 68%的值与平均值之间的标准偏差介于+1和-1之间。这意味着“标准偏差”提供了更多细节。
- 方差用于在一定程度的不确定性下了解计划的行为和实际行为。统计检验使用标准偏差来了解两组变量之间存在的关系
- 方差用于度量围绕中心值的总体中的数据分布。标准差衡量相对于中心值的数据分布
- 两个方差之和(var(A + B)≥var(A)+ var(B)。因此方差不连贯。两个标准差sd(A + B)≤sd(A)+ sd(B)的总和,标准偏差是连贯的,给出了数据偏度的概念,对称分布的偏度值在-1> 0> 1之间。
- 几何均值比算术均值对方差更敏感。几何标准偏差用于查找总体中置信区间的边界。
方差与标准偏差比较表
| 方差 | 标准偏差 | |
| 与均值的均方差 | 方差的平方根 | |
| 测量数据集中的分散 | 它测量均值附近的散布 | |
| 方差不是次加性 | 没有离群值的对称分布的散布量度。 | |
| 方差还可以衡量总体数据的波动性 | 在金融中,标准差通常称为波动率 | |
| 方差衡量结果与均值相差多远。 | 标准偏差测量正常标准偏差与期望值的距离。标准偏差可以作为不确定性的量度 | |
| 在财务中,它有助于衡量绩效与标准之间的实际偏差。 | 标准差是决定股票,共同基金等投资的有用工具,因为它可以衡量与市场波动性相关的风险。 | |
| 可以通过了解方差来采取纠正措施。 | 风险分析过程是对各种股票的标准差计算过程中收集到的结果进行分析和解释,并对结果进行分析以对基金投资做出有效的决策。 |
方差和标准偏差的使用
确定油价的示例
- 一年后油价会是多少?没有一个价格估计。低或高的可能性
- 延误的变化,报废/维修的变化,实际与计划的飞行小时数的变化
- 下一个值会回到平均值还是仅取决于最后一个值?
- 下一个需求量会回到平均水平还是仅取决于最后一个需求量?



多个时期的预测量(20个月的油价)

*该图是考虑一年的数据而制成的,但表中所示数据仅为6个月,该值是随机选择的,可能与油价的市场数据不同。
最后的想法
方差和标准差均从其均值开始衡量数据的传播。它有助于确定共同基金,股票等投资的风险。它是天气预报中有关该期间温度变化的有用工具,并且是用于评估项目风险的蒙特卡洛模拟(Monte Carlo Simulation)工具。