四分位偏差（公式）|实例分步计算

什么是四分位数偏差？

四分位数偏差 基于频率分布中第一四分位数和第三四分位数之间的差异，该差异也称为四分位数范围，该差值除以二称为四分位数偏差或半四分位数范围。

当简单分布或频率分布的第三四分位数和第一四分位数之间的差或方差的一半被接受时，即为四分位数偏差。

公式

四分位数偏差（Q.D.）公式用于统计数据中以衡量价差或换句话说来衡量分散性。这也可以称为半四分位间距。

Q.D. =第3季-第1季/ 2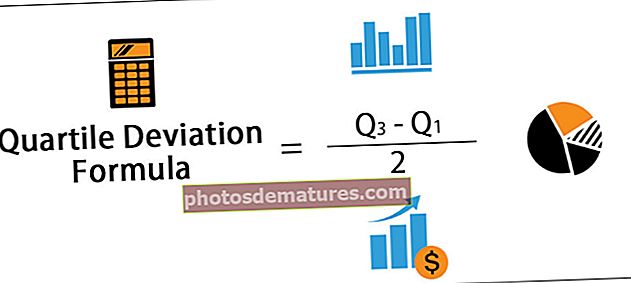

该公式在计算中包括Q3和Q1，分别是前25％的数据和下25％的数据，当将两者之间的差值取而后将这个数字减半时，它将给出扩展或分散的度量。
因此，要计算四分位数偏差，您需要首先找出Q1，然后第二步是找到Q3，然后取两者之差，最后一步是除以2。
这是开放式数据分散的最佳方法之一。

例子

您可以在此处下载此四分位偏差公式Excel模板–四分位偏差公式Excel模板

范例＃1

考虑以下数字的数据集：22、12、14、7、18、16、11、15、12。您需要计算四分位数偏差。

解决方案：

首先，我们需要按升序排列数据以查找Q3和Q1并避免重复。

7, 11, 12, 13, 14, 15, 16, 18, 22

Q1的计算可以如下进行：

Q1 =¼（9 +1）

=¼ (10)

Q1=2.5学期

Q3的计算可以如下进行：

Q3 =¾（9 +1）

=¾ (10)

Q3= 7.5学期

四分位数偏差的计算可以如下进行：

Q1是2的平均值，即11，并且将3和4的差与0.5的乘积相加，即（12-11）* 0.5 = 11.50。
Q3是第7个项与0.5的乘积，第8个和第7个项之间的差是（18-16）* 0.5，结果是16 +1 = 17。

Q.D. =第3季-第1季/ 2

使用四分位数偏差公式，我们得到（17-11.50）/ 2

=5.5/2

Q.D.=2.75.

范例＃2

哈里有限公司是一家纺织品制造商，正在努力建立奖励结构。管理层正在讨论启动一项新计划，但他们首先想知道他们的生产范围是多少。

管理层已收集了每位（平均）员工最近10天的平均每日生产数据。

155, 169, 188, 150, 177, 145, 140, 190, 175, 156.

使用四分位数偏差公式可帮助管理人员找到分散度。

解决方案：

这里的观察数是10，我们的第一步是将数据按升序排列。

140, 145, 150, 155, 156, 169, 175, 177, 188, 190

Q1的计算可以如下进行：

Q1 =第¼（n + 1）个项

=¼ (10+1)

=¼ (11)

Q1= 2.75个学期

Q3的计算可以如下进行：

Q3 =第¾（n + 1）个项

=¾ (11)

Q3= 8.25学期

四分位数偏差的计算可以如下进行：

第二项是145，现在加到0.75 *（150 – 145），这是3.75，结果是148.75
第八项是177，现在加到0.25 *（188 – 177），即2.75，结果是179.75

Q.D. =第3季-第1季/ 2

使用四分位数偏差公式，我们得到（179.75-148.75）/ 2

=31/2

Q.D.=15.50.

例子＃3

瑞安（Ryan）的国际学院希望分析学生分数分数的分布情况。

数据适用于25名学生。

使用四分位数偏差公式可找到以％标记表示的分散。

解决方案：

这里的观察数为25，而我们的第一步将是按升序排列数据。

Q1的计算可以如下进行：

Q1 =第¼（n + 1）个项

=¼ (25+1)

=¼ (26)

Q1= 6.5学期

Q3的计算可以如下进行：

Q3 = 3/4（n + 1）项

=¾ (26)

Q3 = 19.50个学期

四分位偏差或半四分位间距的计算可以如下进行：

第六项是154，现在加到这个0.50 *（156 – 154）的1中，结果是155.00
19项是177，现在加到这个0.50 *（177 – 177）上，它是0，结果是177

Q.D. =第3季-第1季/ 2

使用四分位数偏差公式，我们得到（177-155）/ 2

=22/2

Q.D.= 11.

例子＃4

现在让我们通过一个excel模板为实际示例I确定值。

解决方案：

使用以下数据计算四分位数偏差。

Q1的计算可以如下进行：

Q1=148.75

Q3的计算可以如下进行：

Q3= 179.75

四分位数偏差的计算可以如下进行：

使用四分位数偏差公式，我们得到（179.75-148.75）/ 2

Q.D.将 -

QD = 15.50

photosdematures.com