photosdematures.com

什么是改良的Dietz？

修改后的迪茨（Dietz）指用来确定投资组合的历史绩效的一种方法，该方法是将流出的实际现金流量净额除以平均资本，并在开始时使用投资组合的权重和价值。在简单的Dietz方法中，假定所有现金流量都来自期中，而改良的Dietz方法则不是这种情况。

公式

修改后的Dietz收益率可以使用以下公式进行定义，并解释其中的每个术语：

• ROR （收益率）–这是我们要计算的术语
• 电动势 （最终市场价值）–这是我们要寻找的期限结束后投资组合的价值。
• BMV （开始的市场价值）–这是从日期算起的投资组合的价值，其收益将被计算
• w ^ （投资组合中每个现金流量的权重）–这是投资组合在零和一之间的权重，但仅在它们发生的时期和期末之间。这可以解释为发生流动的时间点与周期结束之间的时间比例。可以使用公式计算
• W = [C-D] / C 其中D是从返回期开始到发生流量的那一天的天数。
• C –该期间的现金流量–这可能不是一个数字，而是该期间发生的一系列现金流量。
• 厕所 =每个现金流量的总和乘以其权重。这是加权现金流量的总和

例子

以下是修改的Dietz方法的一些示例。

范例＃1

让我们考虑一个具有以下条件的非常简单的方案：

• 在投资期开始时，我们的投资组合价值为100万美元。
• 两年后，投资组合的价值已增至230万美元。
• 一年后有50万美元的流入。

现在，我们将计算修改后的Dietz方法将如何用于计算该投资组合的回报。

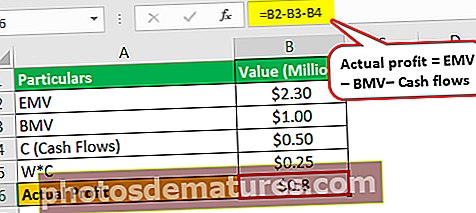
• 实际利润= EMV（230万美元）– BMV（100万美元）–现金流量（50万美元流入）
• =$0.8

这带来了80万美元的利润。

现在让我们看看在这种情况下的平均资本是多少。

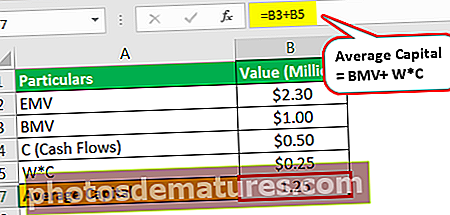
• 平均资本= BMV（100万美元）+ W * C（50万美元* 0.5时间段）
• = 1.25

因此，回报率将为–

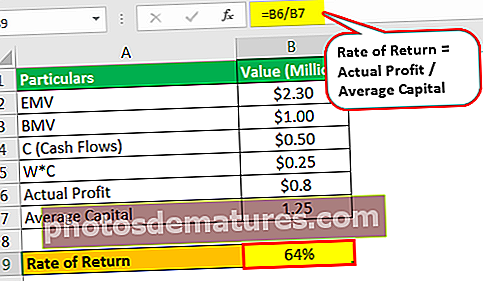
• 收益率=实际利润/平均资本
• = $0.8 / 1.25
• = 64%

范例＃2

修改后的Dietz与时间加权收益率的比较

让我们考虑具有以下投资组合的两个投资者。

1. 投资者A的投资组合为 25万美元 在一年的开始（Jan），并运用他的策略将其转化为 29.8万美元 到同年年底（12月）。但是，他在9月增加了2万5千美元的资本。
2. 投资者B最初的投资组合为 25万美元 在年初（Jan），并使用了他的策略，但最终得到了251k美元 在今年年底。但是，他在9月撤回了2万5千美元。

用肉眼或在我们的脑海中使用基础数学，我们可以看出，投资者B比投资者A的投资能力差。但是，深入地进行计算将使我们完全摆脱故事的另一面。

对于投资者A：

实际利润将为–

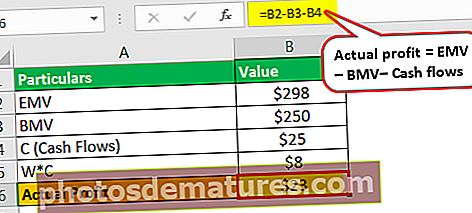
• 实际利润=（298k USD – 250k USD – 25k USD）
• = 23K美元

平均期限为–

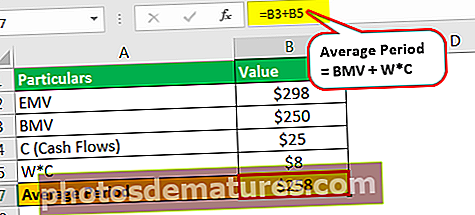
• 平均期间= 25万美元+（2.5万美元* 0.3）
• = 25.8万美元

修改后的Dietz费率将为–

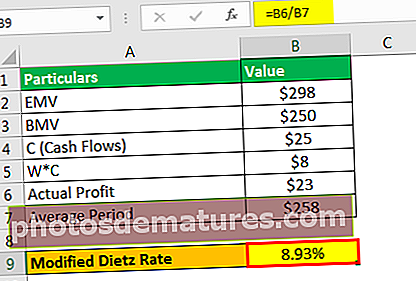
• 修正的Dietz比率= 8.7％

对于投资者B：

实际利润将为–

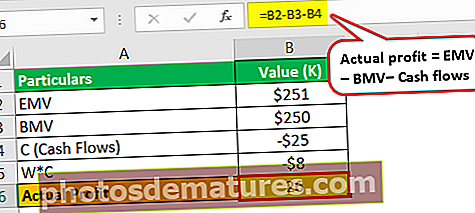
• 实际利润=（21.5万美元– 25万美元+ 2.5万美元）
• = 2.6万美元

平均期限为–

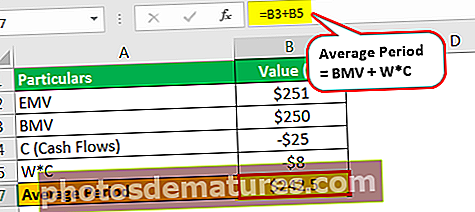
• 平均期间= 25万美元+（-25万美元* 0.3）
• = 242.5千美元

修改后的Dietz费率将为–

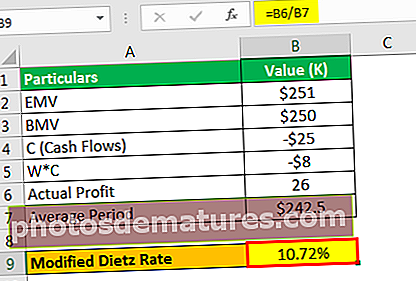
• 修正的Dietz率= 10.72％

以上两种方法的时间加权收益率约为9.5，但经过修改的Dietz给我们带来了不同的结果。这就是投资者将此方法用于报告目的的原因。

好处

• 此方法的主要优点是，它不需要在现金流量的每个日期进行投资组合评估。这有助于分析师轻松确定回报的价值，而无需每次都重新评估。
• 其他时间称量方法无法提供一些性能归因；在这些情况下，改良的Dietz方法很有用。
• 类似于示例2的情况，其中时间加权收益率不是适当的度量。

局限性

• 随着计算的进步，今天的大多数回报都是连续计算的-这些提供了一种更好的分析回报和离开方法的方法，例如Moded Dietz的天真的和基本的方法。
• 假设所有交易在一段时间内在同一时间点同时发生，将导致错误
• 应对负现金流量或平均零现金流量非常困难。

结论

随着金融部门法规的发展，投资者需要更加注意如何计算投资和回报以及如何进行报告。改良Dietz的这种方法在投资回报分析中提供了合理的信心。

修改后的Dietz方法只是为我们提供了有多个流入和流出的投资组合收益的度量。如今，借助高级计算和连续收益管理，此方法已无用。但是，该方法背后的基本概念对于理解收益及其计算方式很有用。