调整后的R平方（含义，公式）|计算调整后的R ^ 2

什么是调整后的R平方？

调整后的R平方是指统计工具，可帮助投资者衡量因变量的方差程度（可以用自变量解释），并且仅考虑那些对变量有影响的自变量的影响的因变量。

调整后的R平方或修改后的R ^ 2决定了因变量的方差程度，可以用自变量解释。修改后的R ^ 2的特长在于它不考虑所有自变量的影响，而仅考虑那些影响因变量变化的因素。修改后的R ^ 2的值也可以是负值，尽管在大多数情况下不是负值。

调整后的回归R平方的计算公式如下所示：

R ^ 2 = {（1 / N）*Σ[（xi-x）*（yi-y）] /（σx*σy）} ^ 2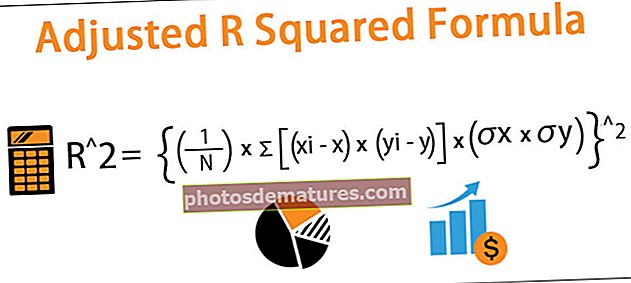

在哪里

请注意

为了在excel中进行计算，需要在excel中提供y和x变量，并且整个输出以及Adjusted R ^ 2均由Excel生成。在特殊情况下，与其他公式不同，很难以文本格式提供输出。

调整后的R平方确定因变量的方差程度，该因变量可以由自变量解释。通过查看调整后的R ^ 2值，可以判断回归方程中的数据是否合适。调整后的R ^ 2越高，回归方程越好，因为它暗示选择用来确定因变量的自变量能够解释因变量的变化。

修改后的R ^ 2的值也可以是负值，尽管在大多数情况下不是负值。在调整后的R方差的情况下，仅当自变量的变化影响因变量的变化时，调整后的R方差的值才会随着添加自变量而上升。这不适用于R ^ 2的情况，仅适用于调整后的R ^ 2的值。

您可以在此处下载此调整后R平方公式Excel模板–调整后R平方公式Excel模板

让我们尝试通过一个示例来理解调整后的R ^ 2的概念。让我们尝试找出卡车司机所覆盖的距离与卡车司机的年龄之间的关系。有人实际上做了回归方程，以验证他对两个变量之间关系的看法是否也被回归方程所验证。

在此特定示例中，我们将看到哪个变量是因变量，哪个变量是自变量。该回归方程式中的因变量是卡车驾驶员的行驶距离，自变量是卡车驾驶员的年龄。通过对变量进行回归，我们得到的调整后的R平方为65％。下面的快照描述了变量的回归输出。数据集和变量在随附的excel工作表中显示。

对于该回归，调整后的R ^ 2值为65％意味着因变量的65％的变化由自变量解释。理想情况下，研究人员将寻找最接近100％的确定系数。

让我们尝试在另一个示例的帮助下理解调整后的R平方的概念。让我们尝试找出班级学生的身高与这些学生的GPA成绩之间的关系。在此特定示例中，我们将看到哪个变量是因变量，哪个变量是自变量。该回归方程中的因变量是学生的GPA，自变量是学生的身高。

通过对变量进行回归，我们可以将调整后的R ^ 2忽略不计或为负。下面的快照描述了变量的回归输出。数据集和变量在随附的excel工作表中显示。

调整后的R ^ 2值对于该回归可以忽略不计，这意味着自变量没有解释因变量的变化。理想情况下，研究人员将寻找最接近100％的确定系数。

调整后的R平方是非常重要的输出，以便确定数据集是否合适。有人实际上做了回归方程，以验证他对两个变量之间关系的看法是否也被回归方程所验证。值越高，回归方程越好，因为它暗示为确定因变量而选择的自变量已正确选择。理想情况下，研究人员将寻找最接近100％的确定系数。