photosdematures.com

收益递减定律定义

收益递减定律指出，单一生产要素的额外数量将导致生产的边际产出减少。法律假定其他因素不变。这意味着，如果X产生Y，那么在添加更多数量的X时会有一点意义，那就是无助于Y数量的少量增加。

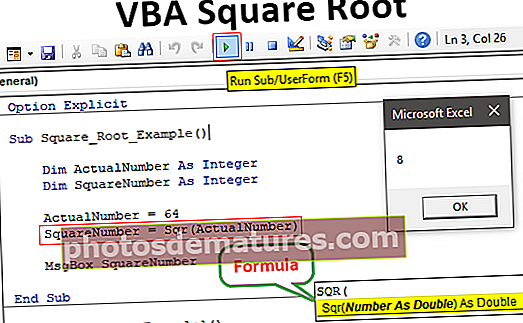
在上面的收益递减规律图中，因子X从1个单位增加到2个单位时，Y的数量增加。但是当X的数量进一步增加到P时，直到Yp为止，生产的速率都会降低。这描述了上面的法律。另一个值得注意的方面是，X的单位进一步增加只会减少Y的产生。因此，增加的投入不仅会影响边际产品，还会影响总产品。该法律主要适用于生产环境。

收益递减法的组成部分

从收益递减规律的定义来看，有三个部分。

1. 生产要素 –产生所需数量的输出的任何输入。关于收益递减规律，一次只考虑一个因素。
2. 边际产品 –每增加一个投入，总产品的增加就称为边际产品。在上图中，Y₂-Y₁ 是边际产品。
3. 总产品 –当通过流程应用输入时，作为总度量的结果或结果就是总产品。

边际收益递减法的假设

• 该法律主要是通过考虑短期生产方案来使用的。这是因为该原理在于将除与产量相关的要素以外的所有其他生产要素保持不变。从长期的生产角度来看，这是不可能的。
• 输入和过程应独立于技术方面，因为技术可以在提高生产效率中发挥作用。

边际收益递减规律的例子

以下是收益递减规律的示例。

您可以在此处下载此收益递减法则Excel模板–收益递减法则Excel模板

范例＃1

假设工厂生产的商品由以下等式给出：

Q = -L3 + 27L2 + 15L

在哪里，

Q是产量

L是劳动投入

描述收益递减法是否适用，如果是，如何适用？

解决方案：

为了检验该法律的适用性，我们将通过假设不同的劳动力投入值来量化生产单位。

我们将Q和L的值绘制在图形上进行分析。 Y轴代表乘积（总计和边际）。 x轴表示劳动单位。

在上面的收益图递减法则中，有两点对法则至关重要：

• 点A –极限边际乘积，以及
• B点–极限总乘积。

以下几点值得注意：

关于边际产出，我们可以将此生产图分为两个阶段。

1. 随着劳动投入的增加，边际产品在劳动者数量之前也增加了，L =9。这是回报增加的阶段。
2. 第十一劳动单元产生的边际产品小于第十劳动单元。这开始了收益递减阶段。

在雇用第20名工人之前，总产品（即Q的数量）不会减少。显然，边际产品从此处进入负收益阶段。

该工厂可雇用9名工人，以保持边际产品的增长率。但是，在注意到总产品下降之前，它最多可以增加19名工人。

范例＃2

一位农民拥有一块小麦田。他开始与一名工人耕种土地。他逐渐将其增加到六名工人，只是发现他的小麦产量没有按比例增加。帮助农民分析所需的最佳劳动力。

解决方案：

通过简单地将小麦产量与使用的劳动力进行比较，可以说边际产量随着部​​署的每增加一个劳动力而在减少。如果我们推断出边际产品并将其呈现给农民，它将看起来像：

这表明边际产品在接受第四劳动者服务之前就增加了。此后，边际产品减少。

因此，农民应在其田地上雇用3名工人来优化其小麦产量。

另一方面，他可以通过不断增加劳动力来最大化自己的总产量。但这是以减少边际产出为代价的。

这两个例子都是从一个好的阶段开始的，在这个阶段我们可以看到“收益递减定律”的优点和局限性。

收益递减法的优势

• 收益递减法则有助于管理人员最大限度地提高劳动力（如上述示例1和2）和其他生产要素，使其达到最佳水平。
• 这种理论还通过将生产成本降至最低来帮助提高生产效率，这从小麦农户的案例中可以明显看出。

收益递减法的局限性

• 尽管在生产活动中很有用，但该法律不能适用于所有形式的生产。当生产要素自然程度降低，因此难以普遍应用时，就会出现制约因素。大多数情况下，该法在农业领域中得到应用。
• 法律假定单一生产要素的所有单位必须相同。但是，这通常不切实际，并成为应用程序中的障碍。在我们上面的示例中，劳动成为特定的投入，其他因素保持不变。

结论

收益递减规律在生产理论中是一个有用的概念。法律可以分为三个阶段：增加收益，减少收益和负收益。生产行业，尤其​​是农业部门，发现该法的适用范围很广。生产者质疑在边际产品图上的何处进行操作，因为第一阶段描述的是利用率不足的生产，而第三阶段则是关于过度利用的投入。因此，达到最佳容量是该法律的基本原理。