采样误差公式|实例分步计算

计算采样误差的公式

采样误差公式 指用于计算统计误差的公式，该公式发生在进行测试的人员未选择代表所考虑总体的样本的情况下，并且根据公式，抽样误差是通过除以将总体乘以样本大小的平方根，然后将结果乘以基于置信区间的Z得分值。

采样误差= Z x（σ/√n）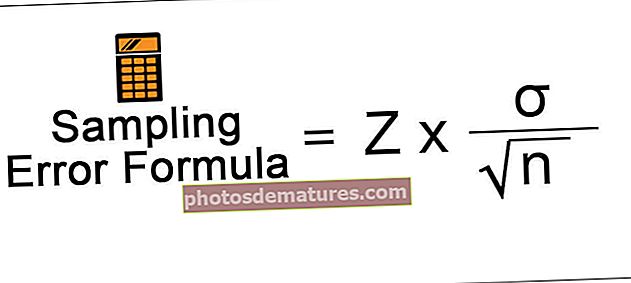

在哪里，

Z是基于置信区间的Z得分值
σ是总体标准差
n是样本的大小

逐步计算采样误差

步骤1：收集了称为人口的所有数据集。计算人口平均值和人口标准偏差。
第2步：现在，需要确定样本大小，并且样本大小必须小于总体，并且不应大于总体。
第三步：确定置信度，因此可以从其表中确定Z分数的值。
第4步：现在，将Z得分乘以总体标准偏差，然后将其除以样本大小的平方根，以得出误差幅度或样本大小误差。

例子

您可以在此处下载此抽样误差公式Excel模板–抽样误差公式Excel模板

范例＃1

假设总体标准偏差为0.30，样本大小为100。在95％置信水平下的抽样误差是多少？

解决方案

在这里，我们得到了总体标准差以及样本的大小，因此我们可以使用以下公式进行计算。

使用以下数据进行计算。

因此，采样误差的计算如下：

抽样误差为–

范例＃2

高塔姆目前正在攻读会计课程，并且已经通过了入学考试。他现在已经注册了中级职位，还将作为实习生加入高级会计师。他将对制造公司进行审计。

他第一次访问的一家公司，被要求检查所有购买条目的账单是否合理。他选择的样本大小为50，而该样本的总体标准偏差为0.50。

根据可用的信息，您需要以95％和99％的置信区间计算采样误差。

解决方案

在这里，我们得到了总体标准差以及样本的大小，因此我们可以使用以下公式进行计算。

95％置信水平的Z分数将为1.96（可从Z分数表中获得）

使用以下数据进行计算。

因此，计算如下

抽样误差为–

95％置信水平的Z分数将为2.58（可从Z分数表中获得）

使用以下数据进行计算。

因此，计算如下

抽样误差为–

随着置信度水平的增加，采样误差也会增加。

例子＃3

在学校中，组织了生物识别会议，以检查学生的健康状况。该课程是由X级标准的学生发起的。 B部共有30名学生。其中12名学生被随机选择进行详细检查，休息，仅进行了一次基础测试。该报告推断，B部门学生的平均身高为154。

解决方案

总体标准差为9.39。根据以上信息，您需要计算90％和95％置信区间的采样误差。

在这里，我们得到了总体标准差以及样本的大小，因此我们可以使用以下公式进行计算。

95％置信水平的Z分数将为1.96（可从Z分数表中获得）

使用以下数据进行计算。

因此，采样误差的计算如下：

抽样误差为–

90％置信水平的Z分数将为1.645（可从Z分数表中获得）

使用以下数据进行计算。

因此，计算如下

抽样误差为–

随着置信度降低，采样误差也降低。

photosdematures.com