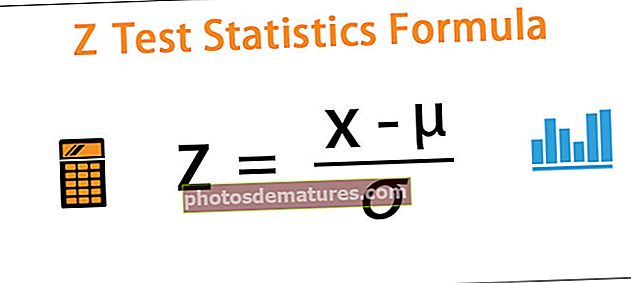统计中的Z检验公式|逐步计算（示例）

在统计中计算Z检验的公式

统计学中的Z检验是指假设检验，用于确定两个样本均值是否不同，以防出现标准差且样本很大。

Z =（x – μ）/ ơ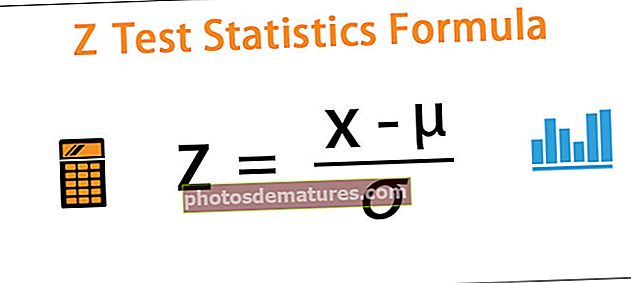

其中x =总体中的任何值

μ=总体平均值
ơ=人口标准差

对于样本，通过从x值中减去样本均值来计算值的z检验统计量的公式，然后将结果除以样本标准差。从数学上讲，它表示为

Z =（x – x_mean）/秒

在哪里

x =样本中的任何值
x_平均值 =样本均值
s =样品标准偏差

Z检验计算（逐步）

总体的z检验统计公式可通过以下步骤得出：

步骤1： 首先，根据在总体均值中捕获的观测值计算总体均值和总体标准差，每个观测值用x表示_一世。总体中观察的总数用N表示。

人口平均值

总体标准差，

第2步： 最后，通过从变量中减去总体平均值来计算z检验统计量，然后将结果除以总体标准偏差，如下所示。

Z =（x – μ）/ ơ

使用以下步骤可以得出样本的z检验统计量公式：

步骤1： 首先，计算样品均值和样品标准偏差与上述相同。在此，样本中的观察总数由n表示，以使n <N。

样本平均值，

样品标准偏差

第2步： 最后，通过从x值中减去样本均值来计算z检验统计量，然后将结果除以样本标准差，如下所示。

Z =（x – x_mean）/秒

例子

您可以在此处下载此Z测试公式Excel模板– Z测试公式Excel模板

范例＃1

让我们假设一所学校中出现参加班级考试的学生人数。测试中的平均分数为75，标准偏差为15。确定在测试中得分为90的David的z检验分数。

鉴于，

总体平均值，μ= 75
总体标准偏差，ơ= 15

因此，z检验统计量可以计算为：

Z =（90 – 75）/ 15

Z测试统计将为–

Z = 1

因此，大卫的考试成绩比总体平均得分高出一个标准偏差，即根据z得分表，比大卫少84.13％的学生得分。

范例＃2

让我们以30名学生为例，他们被选为样本小组的一部分，以进行调查，以查看一周使用了多少支铅笔。根据给定的答案确定第三名学生的z测验分数：3、2、5、6、4、7、4、3、3、8、3、1、3、6、5、2、4 ，3、6、4、5、2、2、4、4、2、8、3、6、7

鉴于，

x = 5，因为第三名学生的回答是5
样本量，n = 30

样本平均值=（3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7）/ 30

均值= 4.17

现在，可以使用上述公式计算样品标准偏差。

ơ= 1.90

因此，第三名学生的z测验分数可以计算为：

Z =（x – x）/ s

Z =（5 –17）/ 1.90
Z = 0.44

因此，第三名学生的使用量是样本平均使用量上方标准偏差的0.44倍，即根据z评分表，有67％的学生比第三名学生使用的铅笔少。

例子＃3

让我们以30名学生为例，他们被选为样本小组的一部分，以进行调查，以查看一周使用了多少支铅笔。根据给定的答案确定第三名学生的Z测验分数：3、2、5、6、4、7、4、3、3、8、3、1、3、6、5、2、4 ，3、6、4、5、2、2、4、4、2、8、3、6、7

以下是用于计算Z检验统计量的数据

您可以参考以下给定的excel工作表，以详细了解Z测试统计信息。

photosdematures.com