Excel中的SIN(公式,示例)|如何在Excel中使用正弦函数?
SIN Excel函数是excel中的内置三角函数,用于计算给定数字的正弦值,或者就三角学而言,用于计算给定角度的正弦值,这里的角度是excel中的数字,并且此函数仅接受单个参数这是提供的输入数字。
Excel中的SIN函数
Excel中的SIN函数计算我们指定的角度的正弦值。 Excel函数中的SIN在Excel中被归类为数学/三角函数。 excel中的SIN始终返回数字值。
在数学和三角学中,SINE是角度的三角函数,在直角三角形中,它等于对边(直角边)的长度除以斜边的长度,并表示为:
正弦Θ=对侧/斜边

正弦Θ= a / h
Excel中的SIN公式
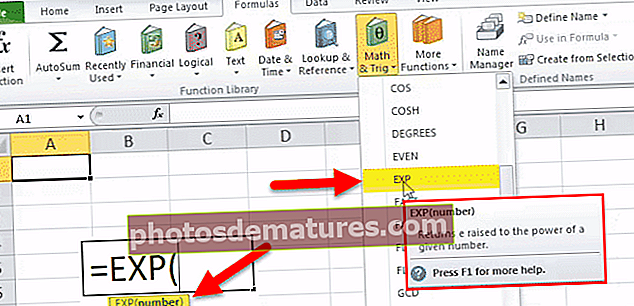
以下是Excel中的SIN公式。

其中number是以弧度形式传递给SIN公式的参数。
如果我们直接在excel函数中将角度传递给SIN,它将不会将其识别为有效参数。例如,如果我们在Excel函数中将30°作为该SIN的参数传递,它将不会将其识别为有效参数。 Excel将显示一条错误消息。

因此,我们需要通过的论点必须在 弧度。
要将角度转换为弧度,有两种方法
- 使用内置的Excel RADIANS函数。 RADIANS函数将度数转换为弧度值。
例如,要将30°转换为弧度,我们将使用此函数,将度数作为数字,将30°视作30。
=拉丹斯(30) 会给弧度0.52

- 在第二种情况下,我们可以使用数学公式将度数转换为弧度。公式是
弧度=度*(π/ 180)(π= 3.14)
在excel中还有一个函数可以返回Pi的值,精确到15位数字,并且该函数是 PI()
因此,对于度到弧度的转换,我们将使用以下公式
弧度=度*(PI()/ 180)
如何在Excel中使用SIN函数?
Excel中的SIN函数非常简单易用。让我们通过一些例子来了解SIN在excel中的工作方式。
您可以在此处下载Excel模板中的此SIN – Excel模板中的SINExcel示例1中的SIN
使用Excel中的SIN函数和Excel中的RADIANS函数计算正弦值 在Excel和PI函数中使用SIN函数计算正弦值 Excel中的正弦函数具有许多实际应用程序。它在体系结构中广泛用于计算几何图形的高度和长度。它还可用于GPS,光学,计算轨迹,基于经纬度地理位置,无线电广播等找到最短路径。甚至将电磁波绘制为正弦和余弦函数图。 假设我们有三个直角三角形,给出了它们的角度和一侧的长度,我们需要计算另一侧的长度。 三角形上所有角度的总和等于180°,因此,我们可以轻松地计算出第三个角度。 我们知道,SinΘ=相对/斜边 因此,对边的长度将是 罪恶Θ*斜边 在Excel中,相对边(垂直边)的长度将通过SIN公式计算 = SIN(弧度(C2))* E2 将上面给出的SIN公式应用于三个三角形,我们可以获得三角形的垂直线的长度 对于第三面(相邻面),我们有两种方法–通过使用毕达哥拉斯定理或从其他角度再次使用Excel函数中的SIN。 根据毕达哥拉斯定理,直角三角形两侧的平方和等于斜边的平方。 斜边2 =对面2 +相邻2 相邻=(斜边2 –对面2)1/2 在excel中,我们将其写为 =电源((电源(斜边,2)-电源(对面,2)),1/2) 应用此公式,我们可以计算相邻边的长度 =电源((电源(E2,2)-电源(F2,2)),1/2) 使用第二种方法,我们可以使用第三个角度的正弦值来计算相邻边的值 如果将三角形向左旋转90°,则相对的一侧将与相邻的一侧互换,并且斜边与相邻的三角形之间的夹角SIN将有助于计算第三侧的值。 = SIN(弧度(D2))* E2 有一幢未知高度的高大建筑物,在某个时间点的太阳光线使A点处的角度为75°,从而使长度为70米的建筑物成为阴影。我们需要找到塔的高度 建筑物的高度将使用excel函数中的SIN进行计算 SIN 75°=建筑物高度/ A点处的阴影长度 因此,建筑物的高度= SIN 75°* A点处的阴影长度 因此,建筑物的高度将为 = SIN(弧度(B3))* B2 建筑物的高度是67.61米 我们有一个三角形形式的平台,对于这两个平台,两个角度分别为30°和70°,我们只知道该三角形的一侧的长度为40米。我们需要找到其他三个边的长度和三角形的周长。 对于三角形,当已知一侧和所有角度时,我们可以通过SINE规则计算另一侧 三角函数中的正弦规则通过SIN公式给出正弦角和三角形边的关系 a / sinα= b / sinß= c / sinδ 在这种情况下, α= 30°,ß= 70°,δ= 180°-(30°+ 70°)= 80°,三角形的一侧b = 40米 要找到三角形的另一边,我们将使用SINE规则 a = Sinα*(b / sinß) 所以, a = SIN(弧度(30))*(B5 / SIN(弧度(70))) a边的长度= 21.28米 同样,第三面c将是 c = Sinδ*(b / sinß) 所以, c = SIN(弧度(80))*(B5 / SIN(弧度(70))) 三角形的三个边长分别为21.28、40、41.92米。 三角形的周长是所有边的总和。 因此,周长将为 = SUM(B5:B7)



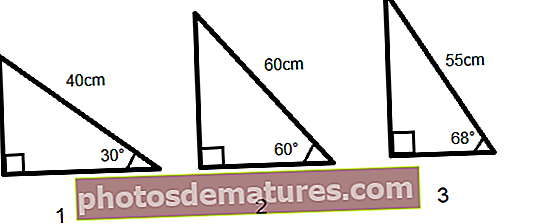








Excel示例2中的SIN



Excel示例3中的SIN