中心极限定理（定义，公式）|计算与示例

中心极限定理定义

中心极限定理指出，随着样本数量的增加，具有任意分布的总体随机变量的随机样本将接近正态概率分布，并假设随着总体样本数量超过30，均值样本的所有观测值的平均值b将接近等于总体的平均值。

中心极限定理公式

我们已经讨论过，当样本大小超过30时，分布呈正态分布的形状。为了确定变量的正态分布，重要的是要知道变量的均值和方差。正态分布可以表示为

X〜N（μ，α）

在哪里

N =没有观测值
µ =观测值的平均值
α=标准偏差

在大多数情况下，观察结果并没有以原始形式揭示太多。因此，标准化观测值以便能够进行比较非常重要。它是在z得分的帮助下完成的。需要计算观察值的Z分数。计算z分数的公式是

Z =（X- µ）/α/√n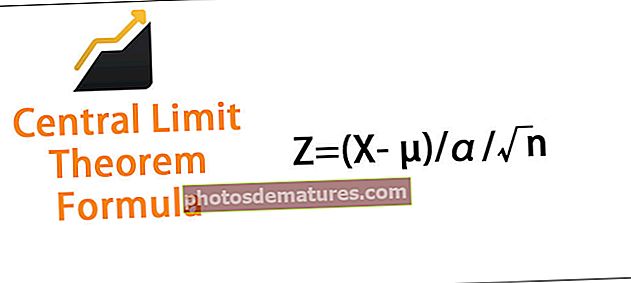

在哪里

Z =观察结果的Z分数
µ =观测值的平均值
α=标准偏差
n =样本量

解释

中心极限定理指出，随着样本大小的增加，具有任意分布的总体随机变量的随机样本将接近正态概率分布。中心极限定理假设，当总体中样本的大小超过30时，该样本的平均值即该样本的所有观察值的平均值将接近于该总体的平均值。同样，当样本大小超过30时，样本的标准偏差将等于总体的标准偏差。因为样本是从整个总体中随机选择的，并且样本的大小大于30，所以它有助于进行假设检验并构建假设检验的置信区间。

中心极限定理公式的示例（带有Excel模板）

您可以在此处下载此中心极限定理公式Excel模板–中心极限定理公式Excel模板

范例＃1

让我们借助示例来了解正态分布的概念。共同基金的平均收益为12％，与共同基金投资的平均收益的标准差为18％。如果我们假设收益的分配是正态分布的，那么让我们解释一下共同基金投资中收益的分配。

鉴于，

投资的平均回报率将为12％
标准偏差为18％

因此，为了找出95％置信区间的收益，我们可以通过将等式求解为

上限= 12 + 1.96（18）= 47％
下限= 12 – 1.96（18）= -23％

结果表明，共同基金的回报率的95％将在47％到-23％的范围内。在此示例中，样本大小是超过30个观察到的收益的随机样本的收益，这将为我们提供共同基金总体收益的结果，因为样本分布将呈正态分布。

范例＃2

继续同一示例，让我们确定90％置信区间的结果是什么

鉴于，

投资的平均回报率将为12％
标准偏差为18％

因此，为了找出置信区间为90％的收益，我们可以通过将等式求解为

上限= 12 + 1.65（18）= 42％
下限= 12 – 1.65（18）= -18％

结果表明，共同基金的回报率中有90％在42％至-18％的范围内。

例子＃3

继续同一示例，让我们确定99％置信区间的结果是什么

鉴于，

投资的平均回报率将为12％
标准偏差为18％

因此，为了找出置信区间为90％的收益，我们可以通过将等式求解为

上限= 12 + 2.58（18）= 58％
下限= 12 – 2.58（18）= -34％

结果表明，共同基金的回报率中有99％将在58％至-34％的范围内。

photosdematures.com