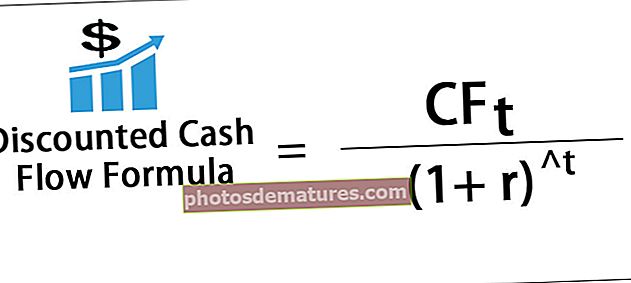有效边界(定义,示例)|什么是有效的边境投资组合?
有效边界定义
有效边界,也称为投资组合边界,是一组理想的或最优的投资组合,它们期望以最小的回报水平获得最高的回报。通过在y轴上绘制预期收益和在x轴上绘制标准偏差作为风险度量来形成此边界。它证明了投资组合的风险和收益之间的权衡。要构建边界,需要考虑三个重要因素:
- 预期收益,
- 方差/标准偏差 作为回报可变性的一种度量,也称为风险和
- 这 协方差 一项资产的收益转换为另一项资产的收益。
该模型是由美国经济学家哈里·马科维兹(Harry Markowitz)在1952年建立的。此后,他花了几年时间研究该模型,最终使他在1990年获得了诺贝尔奖。
有效边界的例子
让我们借助一个数字示例来了解有效边界的构造:
假设特定投资组合中有两个资产A1和A2。计算这两种资产的风险和收益,其预期收益和标准差如下:

现在让我们权衡资产,即如下所示的投资于此类资产的几种投资组合可能性:

使用预期收益和投资组合风险的公式,即
预期收益=(A1的重量* A1的收益)+(A2的重量* A2的收益)
投资组合风险=√[(A12的重量* A12的标准偏差)+(A22的重量* A22的标准偏差)+(2 X相关系数* A1的标准偏差* A2的标准偏差)],
我们可以如下得出投资组合的风险和回报。

通过使用上表,如果我们在X轴上绘制风险,在Y轴上绘制收益,则会得到一个如下图所示的图表,称为有效边界,有时也称为 马科维兹子弹.

在此示例中,为简单起见和易于理解,我们假设投资组合仅由两个资产A1和A2组成。我们可以以类似的方式为多个资产构建投资组合,并将其绘制出来以达到前沿。在上图中,边界外的任何点均次于有效边界上的投资组合,因为它们提供的收益与边界上的那些投资组合相同,但具有较高的风险或较小的收益,具有相同的风险。
从上述有效边界的图形表示中,我们可以得出两个逻辑结论:
- 这是最佳投资组合所在。
- 有效的边界不是一条直线。它是弯曲的。它在Y轴上凹入。
有效边界模型的假设
- 投资者是理性的,并且了解市场的所有事实。这种假设意味着所有投资者都应保持足够的警惕,以了解股票走势,预测收益并据此进行投资。这也意味着,就市场知识而言,该模型假设所有投资者都在同一页上。
- 所有投资者都有一个共同的目标,那就是避免风险,因为他们规避风险,并在可行的情况下尽可能地获得最大的回报。
- 影响市场价格的投资者并不多。
- 投资者拥有无限的借贷能力。
- 投资者以无风险利率借贷。
- 市场是有效的。
- 资产遵循正态分布。
- 市场会迅速吸收信息,并据此采取行动。
- 投资者的决策始终基于预期收益和标准差作为风险度量。
优点
- 这一理论刻画了多元化的重要性。
- 这种有效的边界图可以帮助投资者选择收益最高,投资回报最少的投资组合。
- 它代表了风险回报空间中所有主导的投资组合。
缺点/缺点
- 所有投资者都是理性的并做出正确的投资决策的假设可能并不总是正确的,因为并非所有投资者都会对市场有足够的了解。
- 只有在涉及多元化的概念时,才可以应用该理论或建立边界。在没有多元化的情况下,可以肯定的是该理论将失败。
- 另外,关于投资者拥有无限借贷能力的假设是错误的。
- 资产遵循正态分布模式的假设可能并不总是正确的。实际上,证券可能必须经历远离各自标准偏差的收益,有时就像远离均值的三个标准偏差一样。
- 在构建边界时,不会考虑税收,经纪费,手续费等实际成本。
结论
综上所述,有效边界显示的资产组合具有给定风险水平的最佳预期收益水平。它取决于过去,并且每年都有新数据不断变化。毕竟,过去的数字不一定会在未来继续。
该行上的所有投资组合都是“有效的”,并且不在该行范围内的资产不是最佳的,因为它们对于相同的风险提供较低的收益,或者对于相同的收益水平则具有较高的风险。
尽管该模型有其自身的缺点,例如不可行的假设,但在首次引入该模型时就被指定为具有革命性的。